题目内容
14.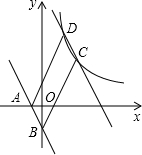 如图,直线AB:y=kx+b(k≠0)过点A(-1,0)和B(0,-2),
如图,直线AB:y=kx+b(k≠0)过点A(-1,0)和B(0,-2),(1)k=-2,b=-2;
(2)若直线AB向右平移与双曲线y=$\frac{{k}_{1}}{x}$交于C、D两点,连接AD交y轴于点E,S△AEB=$\frac{1}{5}$S四边形DEBC,求k1的值和点D、C的坐标.
分析 (1)根据待定系数法即可求得;
(2)分别过C、D作x轴的垂线,垂足为F、G,过C点作CH⊥DG,垂足为H,根据CD∥AB,CD=AB可证△CDH≌△ABO,则CH=AO=1,DH=OB=2,设D(m,n),则C(m+1,n-2),根据k1=(m+1)(n-2)=mn,求得m、n的数量关系,设直线AD解析式为y=ax+c(a≠0),将A、D两点坐标代入求解析式,确定E点坐标,求S△ABE,根据S四边形BCDE=5S△ABE,列方程求m、n的值,即可求得C、D的坐标以及k1的值.
解答 解:(1)∵直线AB:y=kx+b(k≠0)过点A(-1,0)和B(0,-2),
∴$\left\{\begin{array}{l}{-k+b=0}\\{b=-2}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=-2}\\{b=-2}\end{array}\right.$,
故答案是:-2,-2;
(2)如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
∵ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
在△CDH与△ABO中,
$\left\{\begin{array}{l}{∠DHC=∠BOA=90°}\\{∠HDC=∠ABO}\\{DC=BA}\end{array}\right.$,
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=2.
设D(m,n),则C(m+1,n-2),
则(m+1)(n-2)=mn=k1,
解得n=2m+2,则D的坐标是(m,2m+2),
设直线AD解析式为y=ax+b(a≠0),将A、D两点坐标代入得
$\left\{\begin{array}{l}{-a+b=0①}\\{ma+b=2m+2②}\end{array}\right.$,
由①得:a=b,代入②得:mb+b=2m+2,
即b(m+1)=2(m+1),解得b=2,
则 $\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$,
∴y=2x+2,E(0,2),BE=4,
∴S△ABE=$\frac{1}{2}$×BE×AO=2,
∵S四边形BCDE=5S△ABE=5×$\frac{1}{2}$×4×1=10,
∵S四边形BCDE=S△ABE+S四边形BEDM=10,
即2+4×m=10,
解得m=2,
∴n=2m+2=6,
∴C(3,4),D(2,6),
∴k1=mn=2×6=12.
则该反比例函数的解析式为:y=$\frac{12}{x}$.
点评 本题考查了待定系数法求一次函数的解析式以及反比例函数的解析式,一次函数和反比例函数的交点问题.关键是通过作辅助线,将图形分割,寻找全等三角形,利用边的关系设双曲线上点的坐标,根据面积关系,列方程求解.

| A. | (4,5) | B. | (4,-5) | C. | (5,4) | D. | (5,-4) |
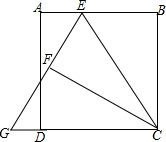 如图,矩形ABCD中,BC=3,且BC>AB,E为AB边上任意一点(不与A,B重合),设BE=t,将△BCE沿CE对折,得到△FCE,延长EF交CD的延长线于点G,则tan∠CGE=$\frac{6t}{9-{t}^{2}}$(用含t的代数式表示).
如图,矩形ABCD中,BC=3,且BC>AB,E为AB边上任意一点(不与A,B重合),设BE=t,将△BCE沿CE对折,得到△FCE,延长EF交CD的延长线于点G,则tan∠CGE=$\frac{6t}{9-{t}^{2}}$(用含t的代数式表示).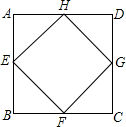 如图,点E,F,G,H分别是正方形ABCD四条边上的中点,求证:四边形EFGH是正方形.
如图,点E,F,G,H分别是正方形ABCD四条边上的中点,求证:四边形EFGH是正方形.