题目内容
11.已知$\sqrt{\frac{x}{y}}$-$\sqrt{\frac{y}{x}}$=$\frac{2}{3}$$\sqrt{3}$,求$\sqrt{\frac{x}{y}}$+$\sqrt{\frac{y}{x}}$.分析 利用完全平方差公式求得($\frac{x}{y}$+$\frac{y}{x}$)的值,然后再根据二次根式的性质和完全平方和公式的变形公式进行计算.
解答 解:∵$\sqrt{\frac{x}{y}}$-$\sqrt{\frac{y}{x}}$=$\frac{2}{3}$$\sqrt{3}$,
∴($\sqrt{\frac{x}{y}}$-$\sqrt{\frac{y}{x}}$)2=($\frac{2}{3}$$\sqrt{3}$)2,即$\frac{x}{y}$+$\frac{y}{x}$-2=$\frac{4}{3}$,
∴$\frac{x}{y}$+$\frac{y}{x}$=$\frac{10}{3}$.
∴($\sqrt{\frac{x}{y}}$+$\sqrt{\frac{y}{x}}$)2=$\frac{x}{y}$+$\frac{y}{x}$+2=$\frac{10}{3}$+2=$\frac{16}{3}$.
又∵$\sqrt{\frac{x}{y}}$+$\sqrt{\frac{y}{x}}$>0,
∴$\sqrt{\frac{x}{y}}$+$\sqrt{\frac{y}{x}}$=$\sqrt{\frac{16}{3}}$=$\frac{4\sqrt{3}}{3}$,即$\sqrt{\frac{x}{y}}$+$\sqrt{\frac{y}{x}}$=$\frac{4\sqrt{3}}{3}$.
点评 本题考查了二次根式的化简求值.解题的关键是求得($\frac{x}{y}$+$\frac{y}{x}$)的值.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
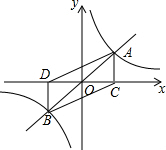 如图,函数y=x与y=$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作x轴垂线,垂足分别为点C、D,则四边形ACBD的面积为8.
如图,函数y=x与y=$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作x轴垂线,垂足分别为点C、D,则四边形ACBD的面积为8.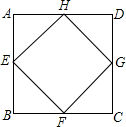 如图,点E,F,G,H分别是正方形ABCD四条边上的中点,求证:四边形EFGH是正方形.
如图,点E,F,G,H分别是正方形ABCD四条边上的中点,求证:四边形EFGH是正方形.