题目内容
18．在学完轴对称图形后，小丽借助圆设计了一个轴对称图形，其中点A、C、D在圆上，四边形BCDE为矩形，如果AB=BC=2，那么圆的半径是$\frac{2\sqrt{3}}{3}$．分析 根据题意得出：△ABC是⊙O的内接等边三角形，过点O作OF⊥BC于点F，连接OBC，根据垂径定理可得出BF的长，故可得出OB的长．
解答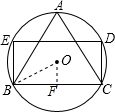 
解：由题意可得：△ABC是⊙O的内接等边三角形，
如图所示：过点O作OF⊥BC于点F，连结OD，
∵△ABC是⊙O的内接等边三角形，AB=BC=2，
∴BF=$\frac{1}{2}$BC=1，∠OBC=30°，
∴OB=$\frac{BF}{cos30°}$=$\frac{1}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{3}}{3}$，
故答案为：$\frac{2\sqrt{3}}{3}$．
点评 本题考查的是轴对称图形以及垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
如图，矩形ABCD中，BC=3，且BC＞AB，E为AB边上任意一点（不与A，B重合），设BE=t，将△BCE沿CE对折，得到△FCE，延长EF交CD的延长线于点G，则tan∠CGE=$\frac{6t}{9-{t}^{2}}$（用含t的代数式表示）．
13．把P1（2，$\sqrt{3}$）向下平移$\sqrt{3}$个单位长度再向左平移2个单位长度到达点P2处，则P2的坐标是（ ）
| A． | （4，0） | B． | （0，0） | C． | （2，2$\sqrt{3}$） | D． | （4，$\sqrt{3}$） |
