题目内容
12.把下列各式分解因式:(1)3(a+b)2+6(a+b);
(2)m(a-b)-n(a-b);
(3)6(x-y)3-3y(y-x)2;
(4)mn(m-n)-m(n-m)2.
分析 (1)提出公因式3(a+b)即可;
(2)提出公因式(a-b)即可;
(3)先将(y-x)2变形为(x-y)2,再提公因式即可;
(4)先将(n-m)2变形为(m-n)2,再提公因式即可.
解答 解:(1)3(a+b)2+6(a+b)=3(a+b)(a+b+2);
(2)m(a-b)-n(a-b)=(a-b)(m-n);
(3)6(x-y)3-3y(y-x)2
=6(x-y)3-3y(x-y)2
=6(x-y)2(x-y-3y)
=6(x-y)2(x-4y);
(4)mn(m-n)-m(n-m)2
=mn(m-n)-m(m-n)2
=m(m-n)(n-m+n)
=m(m-n)(2n-m).
点评 此题主要考查用提公因式法分解因式,找出公因式是解题的关键,对于互为相反数的因式要根据因式的指数进行适当变形.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
17.计算(3a)-1的结果是( )
| A. | $\frac{3}{a}$ | B. | $\frac{1}{3a}$ | C. | 3a | D. | $\frac{a}{3}$ |
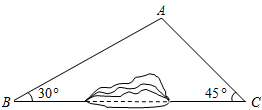 如图所示,因B、C两地之间有一座小山丘阻挡,故无法直接通车.现从B地需经A地才能到达C地.若B、C两地相距6000m,公路AB与BC夹角约为30°,公路AC与BC夹角约为45°,请计算路线B→A→C比BC远了多少米?(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果保留整数)
如图所示,因B、C两地之间有一座小山丘阻挡,故无法直接通车.现从B地需经A地才能到达C地.若B、C两地相距6000m,公路AB与BC夹角约为30°,公路AC与BC夹角约为45°,请计算路线B→A→C比BC远了多少米?(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果保留整数)