题目内容
12.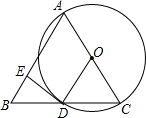 如图,已知△ABC,AB=AC,以边AC为直径作⊙O,BC与圆交于点D,过D作DE⊥AB于E.
如图,已知△ABC,AB=AC,以边AC为直径作⊙O,BC与圆交于点D,过D作DE⊥AB于E.(1)求证:DE为⊙O的切线;
(2)若OD=5,sinB=$\frac{4}{5}$,求BE的长.
分析 (1)连结AD,如图,根据圆周角定理,由AC为直径得到∠ADC=90°,则利用等腰三角形的性质得BD=CD,于是可判断OD为△ABC的中位线,得到OD∥AB,根据平行线的性质易得OD⊥DE,则可根据切线的判定定理判断DE为⊙O的切线;
(2)由OD为△ABC的中位线得到AB=2OD=10,在Rt△ABD中利用正弦定义可计算出AD=8,则利用勾股定理可计算出BD=6,于是可得cosB=$\frac{3}{5}$,然后在Rt△BDE中利用余弦定义可计算出BE的长.
解答 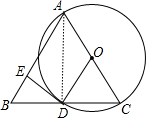 (1)证明:连结AD,如图,
(1)证明:连结AD,如图,
∵AC为直径,
∴∠ADC=90°,
∴AD⊥BC,
而AB=AC,
∴BD=CD,
∵OA=OC,
∴OD为△ABC的中位线,
∴OD∥AB,
∵DE⊥AB,
∴OD⊥DE,
∴DE为⊙O的切线;
(2)解:∵OD为△ABC的中位线,
∴AB=2OD=10,
在Rt△ABD中,∵sinB=$\frac{AD}{AB}$=$\frac{4}{5}$,
∴AD=$\frac{4}{5}$×10=8,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=6,
∴cosB=$\frac{BD}{AB}$=$\frac{6}{10}$=$\frac{3}{5}$,
在Rt△BDE中,∵cosB=$\frac{BE}{BD}$=$\frac{3}{5}$,
∴BE=$\frac{3}{5}$×6=$\frac{18}{5}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了等腰三角形的性质和解直角三角形.

练习册系列答案
相关题目
2.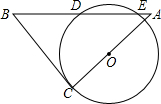 如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
 如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )| A. | 3cm | B. | $\frac{20}{7}$cm | C. | $\sqrt{10}$cm | D. | 2$\sqrt{2}$cm |
10.已知等腰三角形的两边分别为3和7,则此三角形的第三边可能是( )
| A. | 3 | B. | 4 | C. | 6 | D. | 7 |
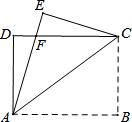 如图,四边形ABCD是矩形,AB=4cm,AD=3cm,把矩形沿直线AC折叠,点B落在点E处交DC于点F,则△ADF和△EFC的周长之和为14cm.
如图,四边形ABCD是矩形,AB=4cm,AD=3cm,把矩形沿直线AC折叠,点B落在点E处交DC于点F,则△ADF和△EFC的周长之和为14cm.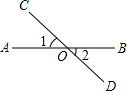 如图,已知点A,O,B在一条直线上,∠1=∠2,你能得到什么结论?试证明你的结论.
如图,已知点A,O,B在一条直线上,∠1=∠2,你能得到什么结论?试证明你的结论. 如图,已知△ABC经过变换能够与△ADC重合,∠BAC=50°,∠ACD=33°.
如图,已知△ABC经过变换能够与△ADC重合,∠BAC=50°,∠ACD=33°. 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O.设AB=a,CG=b(a>b).下列结论:①BG⊥DE;②$\frac{DG}{GC}=\frac{GO}{CE}$;③△BCG∽△EFO;④${(a-b)^2}•{S_{△EFO}}={b^2}•{S_{△DGO}}$.其中正确结论的序号是①③④.(把所有正确结论的序号都填在横线上)
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O.设AB=a,CG=b(a>b).下列结论:①BG⊥DE;②$\frac{DG}{GC}=\frac{GO}{CE}$;③△BCG∽△EFO;④${(a-b)^2}•{S_{△EFO}}={b^2}•{S_{△DGO}}$.其中正确结论的序号是①③④.(把所有正确结论的序号都填在横线上)