��Ŀ����
9�� ��ͼ���ı���ABCD��CEFG���������Σ���G���߶�CD�ϣ�����BG��DE��DE��FG�ཻ�ڵ�O����AB=a��CG=b��a��b�������н��ۣ���BG��DE����$\frac{DG}{GC}=\frac{GO}{CE}$���ۡ�BCG�ס�EFO����${��a-b��^2}•{S_{��EFO}}={b^2}•{S_{��DGO}}$��������ȷ���۵�����Ǣ٢ۢܣ�����������ȷ���۵���Ŷ����ں����ϣ�
��ͼ���ı���ABCD��CEFG���������Σ���G���߶�CD�ϣ�����BG��DE��DE��FG�ཻ�ڵ�O����AB=a��CG=b��a��b�������н��ۣ���BG��DE����$\frac{DG}{GC}=\frac{GO}{CE}$���ۡ�BCG�ס�EFO����${��a-b��^2}•{S_{��EFO}}={b^2}•{S_{��DGO}}$��������ȷ���۵�����Ǣ٢ۢܣ�����������ȷ���۵���Ŷ����ں����ϣ�
���� �ӳ�BG��DE�ڵ�H���ı���ABCD��CEFG���������Σ��õ�BC=DC��CG=CE����BCG=��DCE=90�㣬ͨ����BCG�ա�DCE����֤�â���ȷ����EF��CD��֤�á�DGO�ס�DCE���ɵ�$\frac{DG}{DC}=\frac{GO}{CE}$��������$\frac{DG}{DC}=\frac{GO}{CE}$���ڴ����ɡ�F=��BCD=90�㣬��CBG=��CDE=��FEO���õ���BCG�ס�EFO���ʢ���ȷ�����ݡ�EFO�ס�DGO�����ɵõ������a-b��2S��EFO=b2S��DGO���ʢ���ȷ��
��� ֤�����ӳ�BG��DE�ڵ�H��
���ı���ABCD��CEFG���������Σ�
��BC=DC��CG=CE����BCG=��DCE=90�㣬
�ڡ�BCG�͡�DCE�У�
$\left\{\begin{array}{l}{BC=CD}\\{��BCG=��DCE}\\{CG=CE}\end{array}\right.$��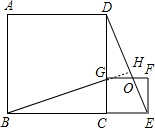
���BCG�ա�DCE��SAS����
���CDE=��CBG��
�ߡ�DGH=��BGC��
���BCG=DHG=90�㣬
��BG��DE���ʢ���ȷ��
��EF��CD��
���GDE=��FEO��
�ߡ�F�T��DCE=90�㣬
���DGO�ס�DCE��
��$\frac{DG}{DC}=\frac{GO}{CE}$��������$\frac{DG}{DC}=\frac{GO}{CE}$��
��ʢڴ���
�ߡ�F=��BCD=90�㣬
��CBG=��CDE=��FEO��
���BCG�ס�EFO���ʢ���ȷ��
�ߡ�EFO�ס�DGO��
��$\frac{{S}_{��EFO}}{{S}_{��DGO}}$=${��\frac{EF}{DG}��}^{2}$=$\frac{{b}^{2}}{{��a-b��}^{2}}$��
�ࣨa-b��2S��EFO=b2S��DGO���ʢ���ȷ��
�ʴ�Ϊ���٢ۢܣ�
���� ���⿼�������������ε��ж������ʣ������ε����ʣ���ȷ�������������ǽ���Ĺؼ���

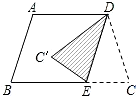 ��ͼ��������ABCD�У�AD��BC��AB=DC����ABC=72�㣬��ƽ���ƶ���AB��DE���ٽ���DCE��DE�۵����á�DC��E�����EDC��Ķ����ǣ�������
��ͼ��������ABCD�У�AD��BC��AB=DC����ABC=72�㣬��ƽ���ƶ���AB��DE���ٽ���DCE��DE�۵����á�DC��E�����EDC��Ķ����ǣ�������| A�� | 72�� | B�� | 54�� | C�� | 36�� | D�� | 30�� |
| A�� | $\left\{\begin{array}{l}x=2y+1\\ y=3-z\end{array}\right.$ | B�� | $\left\{\begin{array}{l}xy=12\\ x+y=7\end{array}\right.$ | ||
| C�� | $\left\{\begin{array}{l}x=3\\ y=4\end{array}\right.$ | D�� | $\left\{\begin{array}{l}\frac{1}{x}+\frac{1}{y}=2\\ 3x-2y=4\end{array}\right.$ |
| A�� | 1��2 | B�� | 1��3 | C�� | 5��1 | D�� | 2��4 |
| A�� | ��a5��2=a10 | B�� | b2+b2=2b2 | C�� | b•b5=b6 | D�� | b5•b5=b25 |
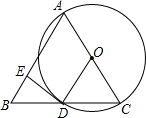 ��ͼ����֪��ABC��AB=AC���Ա�ACΪֱ������O��BC��Բ���ڵ�D����D��DE��AB��E��
��ͼ����֪��ABC��AB=AC���Ա�ACΪֱ������O��BC��Բ���ڵ�D����D��DE��AB��E��