题目内容
4.一次函数y=kx+b,当3≤x≤4时,3≤y≤6,则$\frac{b}{k}$的值是2或-5.分析 由于k的符号不能确定,故应对k>0和k<0两种情况进行解答.
解答 解:当k>0时,此函数是增函数,
∵当3≤x≤4时,3≤y≤6,
∴当x=3时,y=3;当x=4时,y=6,
∴$\left\{\begin{array}{l}{3k+b=3}\\{4k+b=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=3}\\{b=-6}\end{array}\right.$,
∴$\frac{b}{k}=-2$;
当k<0时,此函数是减函数,
∵当3≤x≤4时,3≤y≤6,
∴当x=3时,y=6;当x=4时,y=3,
∴$\left\{\begin{array}{l}{3k+b=6}\\{4k+b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-3}\\{b=15}\end{array}\right.$,
∴$\frac{b}{k}$=-5.
故答案为:-2或-5.
点评 本题考查的是一次函数的性质,在解答此题时要注意分类讨论,不要漏解.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
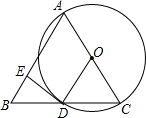 如图,已知△ABC,AB=AC,以边AC为直径作⊙O,BC与圆交于点D,过D作DE⊥AB于E.
如图,已知△ABC,AB=AC,以边AC为直径作⊙O,BC与圆交于点D,过D作DE⊥AB于E. 如图,已知△ABD≌△CAE,∠C=53°,∠ABD=21°.
如图,已知△ABD≌△CAE,∠C=53°,∠ABD=21°.