题目内容
3．
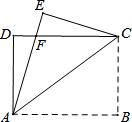如图，四边形ABCD是矩形，AB=4cm，AD=3cm，把矩形沿直线AC折叠，点B落在点E处交DC于点F，则△ADF和△EFC的周长之和为14cm．
分析 根据矩形的性质，得到AB=CD=4cm，AD=BC=3cm，根据折叠的性质，得到AB=AE=4cm，EC=BC=3cm，利用三角形的周长即可解答．
解答 解：∵四边形ABCD是矩形，AB=4cm，AD=3cm，
∴AB=CD=4cm，AD=BC=3cm，
∵把矩形沿直线AC折叠，点B落在点E处交DC于点F，
∴AB=AE=4cm，EC=BC=3cm，
△ADF和△EFC的周长之和=AD+AF+DF+CF+CE+EF=AD+（AF+EF）+（CF+DF）+EC=AD+AE+CD+EC=3+4+4+3=14（cm），
故答案为：14．
点评 本题考查翻折变换，解决本题的关键是根据折叠得到相等的线段．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
11．
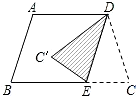如图，在梯形ABCD中，AD∥BC，AB=DC，∠ABC=72°，现平行移动腰AB至DE后，再将△DCE沿DE折叠，得△DC′E，则∠EDC′的度数是（ ）
如图，在梯形ABCD中，AD∥BC，AB=DC，∠ABC=72°，现平行移动腰AB至DE后，再将△DCE沿DE折叠，得△DC′E，则∠EDC′的度数是（ ）| A． | 72° | B． | 54° | C． | 36° | D． | 30° |
8．
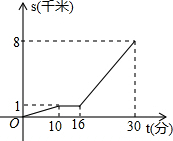小亮从家O，步行到公交站台B，等公交车去学校C，图中的折线表示小亮的行程s（千米）与所花时间t（分）之间的函数关系．下列说法错误的是（ ）
小亮从家O，步行到公交站台B，等公交车去学校C，图中的折线表示小亮的行程s（千米）与所花时间t（分）之间的函数关系．下列说法错误的是（ ）| A． | 他家到公交车站台为1千米 | B． | 他等公交车的时间为6分钟 | ||
| C． | 他步行的速度100米/分钟 | D． | 公交车的速度是350米/分钟 |
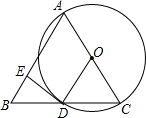如图，已知△ABC，AB=AC，以边AC为直径作⊙O，BC与圆交于点D，过D作DE⊥AB于E．