题目内容
2.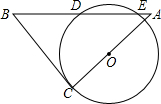 如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )| A. | 3cm | B. | $\frac{20}{7}$cm | C. | $\sqrt{10}$cm | D. | 2$\sqrt{2}$cm |
分析 利用垂径定理得ME=DM=1,利用勾股定理和等腰三角形的性质得OM与DO的关系式,解得结果.
解答  解:过O点作OM⊥AB,
解:过O点作OM⊥AB,
∴ME=DM=1cm,
设MO=h,CO=DO=x,
∵△ABC为等腰直角三角形,AC=BC,
∴∠MAO=45°,
∴AO=$\sqrt{2}$h
∵AO=7-x,
∴$\sqrt{2}h=7-x$,
在Rt△DMO中,
h2=x2-1,
∴2x2-2=49-14x+x2,解得:x=-17(舍去)或x=3,
故选A.
点评 本题主要考查了勾股定理,垂径定理,等腰三角形的性质,作出适当的辅助线,数形结合,建立等量关系是解答此题的关键.

练习册系列答案
相关题目
12.某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
请你选择其中的一种方案,求甲教学楼AB和乙教学楼CD的高度.(结果精确到0.1m)
| 课题 | 测量教学楼高度 | |
| 方案 | 方案一 | 方案二 |
| 测量示意图 | 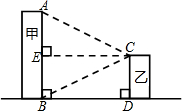 |  |
| 测得数据 | BD=32m,∠ACE=∠BCE=31° | BD=32m,∠DAF=50°,∠CAF=31° |
| 参考数据 | tan31°≈0.60,sin31°≈0.52 cos31°≈0.86 | tan31°≈0.60,tan50°≈1.20, sin50°≈0.77 |
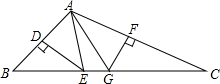 如图,△ABC中,∠BAC=96°,DE、FG分别是AB、AC边的垂直平分线,求∠EAG的度数.
如图,△ABC中,∠BAC=96°,DE、FG分别是AB、AC边的垂直平分线,求∠EAG的度数.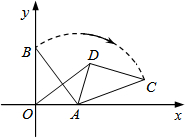 在平面直角坐标系中,已知点A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,连接OD.当∠DOA=∠OBA时,直线CD的解析式为y=-$\frac{7}{24}$x+4.
在平面直角坐标系中,已知点A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,连接OD.当∠DOA=∠OBA时,直线CD的解析式为y=-$\frac{7}{24}$x+4.
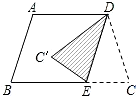 如图,在梯形ABCD中,AD∥BC,AB=DC,∠ABC=72°,现平行移动腰AB至DE后,再将△DCE沿DE折叠,得△DC′E,则∠EDC′的度数是( )
如图,在梯形ABCD中,AD∥BC,AB=DC,∠ABC=72°,现平行移动腰AB至DE后,再将△DCE沿DE折叠,得△DC′E,则∠EDC′的度数是( )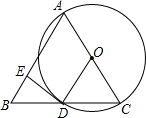 如图,已知△ABC,AB=AC,以边AC为直径作⊙O,BC与圆交于点D,过D作DE⊥AB于E.
如图,已知△ABC,AB=AC,以边AC为直径作⊙O,BC与圆交于点D,过D作DE⊥AB于E.