题目内容
在△ABC中，∠A=20°，∠B=60°，则△ABC的形状是（ ）
A. 等边三角形 B. 锐角三角形
C. 直角三角形 D. 钝角三角形
D
【解析】试题分析：根据三角形的内角和定理求出∠C，即可判定△ABC的形状．
【解析】
∵∠A=20°，∠B=60°，
∴∠C=180°﹣∠A﹣∠B=180°﹣20°﹣60°=100°，
∴△ABC是钝角三角形．
故选D．
练习册系列答案
相关题目
如图，下列说法正确的是 （ ）
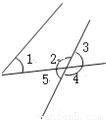
A. ∠1和∠2是内错角 B. ∠1和∠3是内错角
C. ∠1和∠4是内错角 D. ∠1和∠5是内错角
D
【解析】A. ∵∠1和∠2是同旁内角，故不正确；
B. ∵∠1和∠3是同位角，故不正确；
C. ∵ ∠1和∠4不具备特殊位置关系，故不正确；
D. ∵∠1和∠5是内错角，故正确；
故选D. 如图,已知△ABC≌△EDC,指出其对应边和对应角.
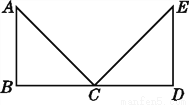
见解析
【解析】试题分析：利用全等三角形的性质分别得出对应点进而得出对应边与对应角关系．
试题解析：△ABC≌△EDC，
∴AB的对应边是ED，AC的对应边是EC，BC的对应边是DC，
∠A的对应角是∠E，∠B的对应角是∠D，∠ACB的对应角是∠ECD. 如图，点C，F在线段BE上，BF=EC，∠1=∠2，请你添加一个条件，使△ABC≌△DEF，并加以证明．（不再添加辅助线和字母）
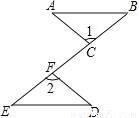
见解析
【解析】试题分析：先求出BC=EF，添加条件AC=DF，根据SAS推出两三角形全等即可．
AC=DF．
证明：∵BF=EC，
∴BF﹣CF=EC﹣CF，
∴BC=EF，
在△ABC和△DEF中
∴△ABC≌△DEF（SAS）． 一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上，BC与DE交于点M.如果∠ADF＝100°，那么∠BMD为( )
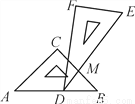
A. 95° B. 85° C. 90° D. 100°
B
【解析】∵∠ADF=100°，∠EDF=30°，
∴∠MDB=180°-∠ADF-∠EDF=180°-100°-30°=50°，
∴∠BMD=180°-∠B-∠MDB=180°-45°-50°=85°，
故选B. 若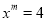
， 
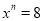，求
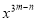的值。
8
【解析】试题分析：根据已知条件，逆用同底数幂的除法法则计算即可.
试题解析：
∵， ，
∴ 
________．
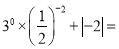6
【解析】根据零指数幂的性质和负整指数幂性质、绝对值，可得=1×4+2=6.
故答案为：6. [(2x－y)(2x＋y)＋y(y－6x)＋x(6y－2)]÷2x，其中x＝1009.
2017
【解析】试题分析：先计算中括号内的式子，把结果化为最简后，再利用多项式除以单项式的运算法则计算，最后代入求值即可.
试题解析：
[(2x－y)(2x＋y)＋y(y－6x)＋x(6y－2)]÷2x，
=
=
=2x-1
当x＝1009时，原式=2018-1=2017. 下列去括号正确的是（ ）
A. a-(b+c)=a-b+c B. a-(b-c)=a-b-c C. a-(b+c)=a+b-c D. a-(-b-c)=a+b+c
D
【解析】试题分析：A、a－(b＋c)＝a－b－c，故此选项错误；
B、a－(b－c)＝a－b＋c，故此选项错误；
C、a－(b＋c)＝a－b－c，故此选项错误；
D、a－(－b－c)＝a＋b＋c，故此选项正确．
故选D．