题目内容
如图,已知△ABC≌△EDC,指出其对应边和对应角.
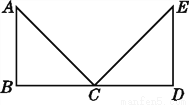
见解析
【解析】试题分析：利用全等三角形的性质分别得出对应点进而得出对应边与对应角关系．
试题解析：△ABC≌△EDC，
∴AB的对应边是ED，AC的对应边是EC，BC的对应边是DC，
∠A的对应角是∠E，∠B的对应角是∠D，∠ACB的对应角是∠ECD.
练习册系列答案
阅读快车系列答案
相关题目
如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?
解:a与c平行.
理由:因为∠1=∠2( ),
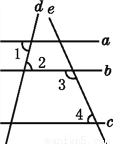
所以a∥b ( ).
因为∠3+∠4=180°( ),
所以b∥c ( ).
所以a∥c ( ).
已知;内错角相等,两直线平行;已知;同旁内角互补,两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行
【解析】试题分析：根据平行线的性质得出a∥b，b∥c，即可推出答案．
试题解析：a∥c，
理由是：∵∠1=∠2(已知)，
∴a∥b(内错角相等，两直线平行)，
∵∠3+∠4=180°(已知)，
∴b∥c(同旁内角互补，两直线平行)，
∴a... 如图,在△ABC中,∠BAC=4∠ABC=4∠C,BD⊥AC交CA的延长线于点D,求∠ABD的度数.
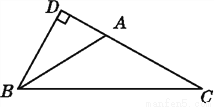
30°.
【解析】试题分析：利用三角形的内角和为180°即可得到∠ABC或∠C的度数，进而利用外角可求得∠DAB的度数，从而求得∠ABD的度数．
试题解析：∵∠BAC=4∠ABC=4∠C，
∴∠BAC+∠ABC+∠C=180°，
即∠C=∠ABC=180×=30°，
∴∠DAB=∠C+∠ABC=30°+30°=60°，
∵BD⊥AC，
∴∠BDA=90°，... 如图，AD=BC，DC=AB，AE=CF，找出图中的一对全等三角形，并说明你的理由。
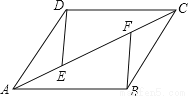
△ABC≌△CDA
【解析】试题分析：全等三角形之一是△ABC≌△CDA，理由是根据AB=DC，AD=BC，AC=AC，根据全等三角形的判定定理SSS推出即可．
试题解析：△ABC≌△CDA．
理由是：在△ABC和△CDA中，
∵
∴△ABC≌△CDA（SSS）. 如图,△ADF≌△CBE,且点E,B,D,F在一条直线上.试判断:
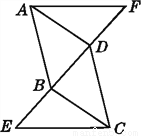
(1)AD与BC的位置关系(并加以说明);
(2)BF与DE的数量关系,并说明理由.
(1)AD∥BC；(2)BF=DE
【解析】试题分析：（1）由“已知全等三角形的对应角相等”推知∠ADF=∠CBE，则等角的补角相等，即内错角∠ADB=∠CBD，则易证得AD∥BC；
（2）由“已知全等三角形的对应边相等”推知BE=DF，则根据等式的性质得到BE+BD=DF+BD，即BF=DE．
试题解析: (1)AD∥BC.理由如下：
∵△ADF≌△CBE，
∴∠A... 如图所示，△ABC≌△CDA，AC=7 cm，AB=5 cm，BC=8 cm，则AD的长是（ ）
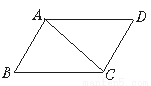
A.7 cm B.5 cm C.8 cm D.无法确定
C
【解析】
试题分析：根据全等三角形的性质即可得到结果.
∵△ABC≌△CDA，
∴BC=AD=8 cm，
故选C. 如图,有6个条形方格图,图中由实线围成的图形中,全等图形有:①与___________;②与___________.
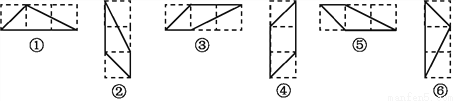
⑥ ③⑤
【解析】由全等图形的定义并观察图形可得①和⑥是全等图形,②、③和⑤是全等图形.
故答案为：⑥、③⑤ 在△ABC中，∠A=20°，∠B=60°，则△ABC的形状是（ ）
A. 等边三角形 B. 锐角三角形
C. 直角三角形 D. 钝角三角形
D
【解析】试题分析：根据三角形的内角和定理求出∠C，即可判定△ABC的形状．
【解析】
∵∠A=20°，∠B=60°，
∴∠C=180°﹣∠A﹣∠B=180°﹣20°﹣60°=100°，
∴△ABC是钝角三角形．
故选D． 在代数式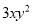
， 
， 
， 
， 
， 
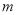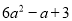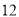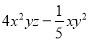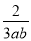中，单项式有___个，多项式有____个。
3 2
【解析】单项式有：3xy2，m，12，共3个，多项式有：6a2-a+3，4x2yz-xy2，共2个.
故答案为：3，2.