题目内容
17.解二元一次方程组(1)$\left\{\begin{array}{l}{3x-2y=-1}\\{x+3y=1}\end{array}\right.$ (用代入消元法);
(2)$\left\{\begin{array}{l}{2x+3y=-7}\\{3x-3y=12}\end{array}\right.$(用加减消元法);
(3)$\left\{\begin{array}{l}{4x-3y=39}\\{7x+4y=-15}\end{array}\right.$;
(4)$\left\{\begin{array}{l}{\frac{x-2y}{4}-\frac{5x-3y}{3}=\frac{5}{6}}\\{\frac{x-2y}{2}+\frac{5x-3y}{6}=\frac{7}{12}}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可;
(3)方程组利用加减消元法求出解即可;
(4)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x-2y=-1①}\\{x+3y=1②}\end{array}\right.$,
由②得:x=-3y+1③,
把③代入①得:-9y+3-2y=-1,
移项合并得:11y=4,
解得:y=$\frac{4}{11}$,
把y=$\frac{4}{11}$代入③得:x=-$\frac{1}{11}$,
则方程组的解为$\left\{\begin{array}{l}{x=-\frac{1}{11}}\\{y=\frac{4}{11}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+3y=-7①}\\{3x-3y=12②}\end{array}\right.$,
①+②得:5x=5,即x=1,
把x=1代入①得:y=-3,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-3}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{4x-3y=39①}\\{7x+4y=-15②}\end{array}\right.$,
①×4+②×3得:37x=111,即x=3,
把x=3代入①得:y=-9,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-9}\end{array}\right.$;
(4)方程组整理得:$\left\{\begin{array}{l}{-17x+6y=10①}\\{16x-18y=7②}\end{array}\right.$,
①×3+②得:-35x=37,即x=-$\frac{37}{35}$,
把x=-$\frac{37}{35}$代入②得:y=$\frac{93}{70}$,
则方程组的解为$\left\{\begin{array}{l}{x=-\frac{37}{35}}\\{y=\frac{93}{70}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,解三元一次方程组,熟练掌握运算法则是解本题的关键.

| A. | -1 | B. | 1 | C. | 52005 | D. | -52005 |
| A. | 4x2y+4y2x=8x2y | B. | 2abc+2ab=4ab | C. | 7ab-3ba=4ab | D. | a3+a2=a5 |
| A. | x2=21 | B. | $\frac{1}{2}$x(x+1)=21 | C. | $\frac{1}{2}{x}^{2}$=21 | D. | x(x-1)=21 |
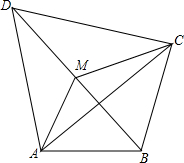 如图,已知四边形ABCD,M是BD的中点.
如图,已知四边形ABCD,M是BD的中点.