题目内容
7.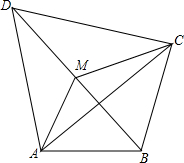 如图,已知四边形ABCD,M是BD的中点.
如图,已知四边形ABCD,M是BD的中点.(1)求证:四边形ABCM的面积等于四边形ABCD的面积的一半;
(2)试过点C画一条直线,把四边形ABCD分成等积的两部分.
分析 (1)依据等底同高的两三角形面积相等进行证明即可;
(2)过点M作ME∥AC,交AD于E,连接CE,CE,依据同底等高的两三角形面积相等可知EC将四边形ABCD分成等积的两部分.
解答 解:(1)如图所示:过点作CE⊥BD,垂足为E.
∵M是BD的中点,
∴MD=BM.
∴$\frac{1}{2}MD•EC•\frac{1}{2}MB•EC$,即S△DCM=S△BCM.
同理:SADM=S△ABM.
∴四边形ABCM的面积等于四边形ABCD的面积的一半.
(2)如图2所示:过点M作ME∥AC,交AD于点E,连接EC.
EC即为所求.
点评 本题主要考查的是作图--应用与设计,掌握等底等高的两个三角形面积相等是解题的关键.

练习册系列答案
相关题目
5.在下列解方程的变形过程中,正确的是( )
| A. | 由x-5=7得x=-5-7 | B. | 由2(x-3)=7得2x-3=7 | ||
| C. | 由$\frac{x-1}{2}-\frac{3x-1}{6}=1$得3(x-1)-(3x-1)=6 | D. | 由$\frac{x}{0.3}-\frac{x}{0.6}=1$得$\frac{10x}{3}-\frac{10x}{6}=10$ |
2.已知点A(-3,-2),则A关于x轴的对称点B的坐标为( )
| A. | (3,2) | B. | (3,-2) | C. | (-2,-3) | D. | (-3,2) |
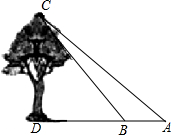 如图,从树顶C望地面上的AB两点,测得它们的俯角分别是45°和30°,已知AB=200m,点B在AD上,求树高CD.
如图,从树顶C望地面上的AB两点,测得它们的俯角分别是45°和30°,已知AB=200m,点B在AD上,求树高CD. 已知二次函数图象的顶点在原点O,对称轴为y轴.一次函数y=kx+1的图象与二次函数的图象交于A、B两点(A在B的左侧),且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.
已知二次函数图象的顶点在原点O,对称轴为y轴.一次函数y=kx+1的图象与二次函数的图象交于A、B两点(A在B的左侧),且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.