要组织一次篮球联赛.赛制为单循环形式.计划安排21场比赛．设参赛球队的个数为x.则根据题意所列的方程是( )A．x2=21B．$\frac{1}{2}$x(x+1)=21C．$\frac{1}{2}{x}^{2}$=21D．x(x-1)=21 题目和参考答案——青夏教育精英家教网—

题目内容

7．要组织一次篮球联赛，赛制为单循环形式（每两队之间都赛一场），计划安排21场比赛．设参赛球队的个数为x，则根据题意所列的方程是（　　）

A．

x²=21

B．

$\frac{1}{2}$x（x+1）=21

C．

$\frac{1}{2}{x}^{2}$=21

D．

x（x-1）=21

分析赛制为单循环形式（每两队之间都赛一场），x个球队比赛总场数=$\frac{1}{2}$x（x+1），即可列方程．

解答解：设参赛球队的个数为x，则每个队都要赛（x-1）场，但两队之间只有一场比赛，
$\frac{1}{2}$x（x+1）═21．
故选B．

点评本题考查了由实际问题抽象出一元二次方程，解决本题的关键是读懂题意，得到总场数的等量关系．

练习册系列答案

	A．	12abc-9a²b²=3abc（4-3ab）		B．	3m²n-3mn+6n=3n（m²-m+2）
	C．	-x²+xy-xz=x（x+y-z）		D．	a²b+5ab-b=b（a²+5a）

15．将下列各数填入相应的集合内．
-7，0.32，$\frac{1}{3}$，0，$\sqrt{8}$，$\sqrt{\frac{1}{2}}$，$\root{3}{125}$，π，0.1010010001…
①有理数集合{                  …}
②无理数集合{                  …}
③负实数集合{                  …}．

2．

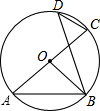如图，AC是⊙O的直径，点B，D在⊙O上，那么图中等于∠BOC一半的角有（　　）

12．现有甲、乙两个合唱队队员的平均身高为170cm，方差分别是S_甲²、S_乙²，且S_甲²＞S_乙²，则两个队的队员的身高较整齐的是乙．

19．如图，在平面直角坐标系中，点M、B的坐标分别为（6，8）、（24，0），过点O作⊙M，C、D为⊙M上两点，$\widehat{OC}$=$\widehat{OA}$，E是BD中点．
（1）判断AE与AC的数量关系，并说明理由；
（2）设F是AC的中点，P为⊙M上一点，且PF=PE，求点P的坐标；
（3）是否存在点C，使AE与⊙M相切？如果存在，求点C的坐标；如果不存在，请说明理由．

16．

如图所示，在等边△ABC中，BE=CF，连接AE，BF相交于点Q，则∠AQF的度数是（　　）

17．已知一次函数y=$\frac{2}{3}$x+m和y=-$\frac{1}{2}$x+n的图象都过点A（-2，0），且与y轴分别交于B、C两点，那么△ABC的面积是（　　）

试题分类