题目内容

12．若$\sqrt{a+b+5}$+|2a-b+1|=0，则（b-a）2005的值为（　　）
A．-1B．1C．52005D．-52005

分析 首先根据非负数的性质可求出a、b的值，进而可求出（b-a）2005的值．

解答 解：∵$\sqrt{a+b+5}$+|2a-b+1|=0，
∴a+b+5=0，2a-b+1=0，
∴a=-2，b=-3；
因此（b-a）2005=（-3+2）2005=-1．
故选A．

点评 本题考查了非负数的性质，初中阶段有三种类型的非负数：绝对值、偶次方、二次根式（算术平方根）．当它们相加和为0时，必须满足其中的每一项都等于0．

练习册系列答案
相关题目
2．已知二次函数图象的顶点在原点O，对称轴为y轴．一次函数y=kx+1的图象与二次函数的图象交于A、B两点（A在B的左侧），且A点坐标为（-4，4）．平行于x轴的直线l过（0，-1）点．
（1）求一次函数与二次函数的解析式；
（2）求点B的坐标；
（3）判断以线段AB为直径的圆与直线l的位置关系，并给出证明；
（4）把二次函数的图象向右平移2个单位，再向下平移t个单
位（t＞0），二次函数的图象与x轴交于M、N两点，一次函数图象交y轴于F点．当t为何值时，过F、M、N三点的圆的面积最小？最小面积是多少？
3．方程3x+2y=13的所有正整数解是$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$，$\left\{\begin{array}{l}{x=1}\\{y=5}\end{array}\right.$．
20．在反比例函数y=$\frac{k-2015}{x}$图象的每一支曲线上，y都随x的增大而减小，则k的取值范围是k＞2015．
7．已知$\sqrt{5.217}$=2.284，$\sqrt{52.17}$=7.223，则$\sqrt{0.05217}$=0.2284，若$\sqrt{x}$=72，23，则x的值为5217．
17．解二元一次方程组
（1）$\left\{\begin{array}{l}{3x-2y=-1}\\{x+3y=1}\end{array}\right.$ （用代入消元法）；
（2）$\left\{\begin{array}{l}{2x+3y=-7}\\{3x-3y=12}\end{array}\right.$（用加减消元法）；
（3）$\left\{\begin{array}{l}{4x-3y=39}\\{7x+4y=-15}\end{array}\right.$；
（4）$\left\{\begin{array}{l}{\frac{x-2y}{4}-\frac{5x-3y}{3}=\frac{5}{6}}\\{\frac{x-2y}{2}+\frac{5x-3y}{6}=\frac{7}{12}}\end{array}\right.$．
4．把二次函数y=x2的图象向右平移2个单位，再向下平移5个单位，所得图象对应的函数式是（　　）
A．y=（x-2）2-5B．y=（x-2）2+5C．y=（x+2）2-5D．y=（x+2）2-5
1．若3+$\sqrt{6}$的小数部分为m，3-$\sqrt{6}$的小数部分为n，则m+n的值为1．
2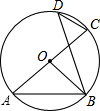．如图，AC是⊙O的直径，点B，D在⊙O上，那么图中等于∠BOC一半的角有（　　）
A．4个B．3个C．2个D．l个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网