题目内容
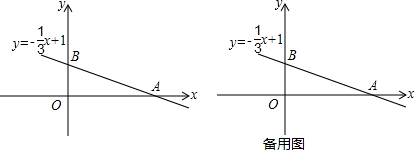
如图,已知一次函数y=-
x+1的图象与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标及线段的AB的长度;
(2)在如图的坐标系中给△AOB拼接一个直角三角形(不重叠且无缝隙的拼接),使得拼成的图形是以AB为边的等腰△ABP的顶点P的坐标.
| 1 |
| 3 |
(1)求A、B两点的坐标及线段的AB的长度;
(2)在如图的坐标系中给△AOB拼接一个直角三角形(不重叠且无缝隙的拼接),使得拼成的图形是以AB为边的等腰△ABP的顶点P的坐标.

考点:一次函数综合题
专题:常规题型
分析:(1)根据直线AB的解析式可以求得A,B的坐标,即可求得AB的长度;
(2)分3种情况讨论:①BP=BA,②AP=AB,③PA=PB.
(2)分3种情况讨论:①BP=BA,②AP=AB,③PA=PB.
解答:解:(1)直线AB解析式为y=-
x+1,
∵x=0时,y=1,
∴点B坐标为(0,1)
∵y=0时,x=3,
∴点A坐标为(3,0)
AB=
=
.
(2)如图,
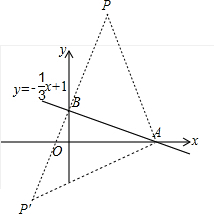
①点B为直角,则存在点P和P'满足BP=BA,
∵PB⊥AB,
∴直线PB的斜率为3,
设直线PB为y=3x+b,代入点B得:b=1,
∴直线PB解析式为y=3x+1,
设P点坐标为(x,3x+1),则x2+(3x+1-1)2=10,
解得x=1或-1,y=4或-2,
∴P点坐标为(1,4),(-1,-2).
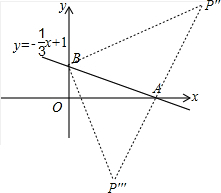
②点A为直角,则存在点P满足满足AP=BA,
∵PB⊥AB,
∴直线AP的斜率为3,
设直线PA为y=3x+b,代入点A得:b=-9,
∴直线PB解析式为y=3x-9,
设P点坐标为(x,3x-9),
则(x-3)2+(3x-9)2=10,
解得x=2或4,y=-3或3.
∴P点坐标为(2,-3),(4,3).
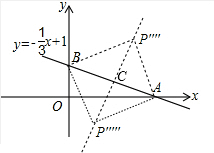
③C为AB中点,点C中点为(
,
)则存在点P满足满足CP=BC,
∵PC⊥AB,
∴直线CP的斜率为3,
设直线PC为y=3x+b,代入点C得:b=-4,
∴直线PC解析式为y=3x-4,
设P点坐标为(x,3x-4),
则(x-
)2+(3x-4-
)2=
,
解得x=1或2,y=-1或2,
∴P点坐标为(1,1),(2,2).
∴P点坐标为(1,1)或(2,2)或(1,4)或(-1,-2)或(2,-3)或(4,3).
| 1 |
| 3 |
∵x=0时,y=1,
∴点B坐标为(0,1)
∵y=0时,x=3,
∴点A坐标为(3,0)
AB=
| 12+32 |
| 10 |
(2)如图,

①点B为直角,则存在点P和P'满足BP=BA,
∵PB⊥AB,
∴直线PB的斜率为3,
设直线PB为y=3x+b,代入点B得:b=1,
∴直线PB解析式为y=3x+1,
设P点坐标为(x,3x+1),则x2+(3x+1-1)2=10,
解得x=1或-1,y=4或-2,
∴P点坐标为(1,4),(-1,-2).

②点A为直角,则存在点P满足满足AP=BA,
∵PB⊥AB,
∴直线AP的斜率为3,
设直线PA为y=3x+b,代入点A得:b=-9,
∴直线PB解析式为y=3x-9,
设P点坐标为(x,3x-9),
则(x-3)2+(3x-9)2=10,
解得x=2或4,y=-3或3.
∴P点坐标为(2,-3),(4,3).

③C为AB中点,点C中点为(
| 3 |
| 2 |
| 1 |
| 2 |
∵PC⊥AB,
∴直线CP的斜率为3,
设直线PC为y=3x+b,代入点C得:b=-4,
∴直线PC解析式为y=3x-4,
设P点坐标为(x,3x-4),
则(x-
| 3 |
| 2 |
| 1 |
| 2 |
| 10 |
| 4 |
解得x=1或2,y=-1或2,
∴P点坐标为(1,1),(2,2).
∴P点坐标为(1,1)或(2,2)或(1,4)或(-1,-2)或(2,-3)或(4,3).
点评:本题考查了一次函数与平面直角坐标系交点的求解,考查了等腰直角三角形的腰长相等的性质.本题中分类讨论点P的位置是解题的关键.

练习册系列答案
相关题目
 已知如图,在四边形ABCD中,∠A=90°,AB=3cm,BC=13cm,CD=12cm,AD=4cm,求四边形ABCD的面积.
已知如图,在四边形ABCD中,∠A=90°,AB=3cm,BC=13cm,CD=12cm,AD=4cm,求四边形ABCD的面积.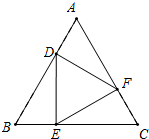 如图,在边长为3的等边△ABC中,D、E、F分别是AB、BC、AC上的点,AD=BE=CF=1.
如图,在边长为3的等边△ABC中,D、E、F分别是AB、BC、AC上的点,AD=BE=CF=1. 如图,四边形ABCD是一个长方形的台球桌,台球桌上还剩一个黑球没有被打进球袋,在点P的位置,现在轮到你打,你应该把在点Q位置的白球打到AB边上的哪一个点,才能反弹回来撞到黑球?试作图说明.
如图,四边形ABCD是一个长方形的台球桌,台球桌上还剩一个黑球没有被打进球袋,在点P的位置,现在轮到你打,你应该把在点Q位置的白球打到AB边上的哪一个点,才能反弹回来撞到黑球?试作图说明.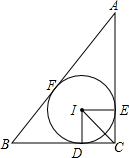 如图,在△ABC中,∠C=90°,内切圆⊙I与AC、BC分别相切于点E,D.
如图,在△ABC中,∠C=90°,内切圆⊙I与AC、BC分别相切于点E,D.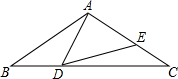 如图,△ABC中,AB=AC=2,∠B=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
如图,△ABC中,AB=AC=2,∠B=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.