题目内容

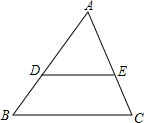如图，已知DE∥BC，AD=5，DB=3，则S△ADE：S四边形DBCE=
 
．
考点：相似三角形的判定与性质
专题：
分析：由DE∥BC证明△ADE∽△ABC，根据“相似三角形面积的比等于相似比的平方”可得两三角形面积比，然后根据比例的性质求解．
解答：解：∵DE∥BC，
∴△ADE∽△ABC，相似比是5：8，
∴
S△ADE
S△ABC
=
25
64
，
∴S△ADE：S四边形DBCE=
25
39
．
故答案是：
25
39
．
点评：本题考查对相似三角形性质的理解，相似三角形面积的比等于相似比的平方．
练习册系列答案
相关题目
如图，已知抛物线y=ax2-
3
2
x+c与x轴相交于A、B两点，并与直线y=
1
2
x-2交于B、C两点，其中点C是直线y=
1
2
x-2与y轴的交点，连接AC．
（1）求抛物线的解析式；
（2）证明：△ABC为直角三角形．
如图，在边长为3的等边△ABC中，D、E、F分别是AB、BC、AC上的点，AD=BE=CF=1．
（1）求证：△DEF是等边三角形；
（2）猜想DE与BC的位置关系，并加以验证．
如图，在△ABC中，∠C=90°，内切圆⊙I与AC、BC分别相切于点E，D．
（1）试判断四边形CDIE的形状，并说明理由；
（2）若此直角三角形的两条直角边的长分别为9和40，求线段CI的长．
如图，等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA=CQ时，连PQ交AC边于D，
①猜想DE与AB的关系？并加以证明；
②若P是AB延长线一点，Q为BC一点，其他条件不变，结论成立吗？画图并证明．
（友情引导：若不知道，你可以动手去量发现结论．若不会，P是动点，你可以把P运动到特殊的地方，发现现在可利用什么性质？接下来证明．发现缺少什么？就补什么？若还不会，你能发现有线段相等吗？尝试证明，你会有惊喜．）
如图，△ABC中，AB=AC=2，∠B=40°．点D在线段BC上运动（点D不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E．
（1）当∠BAD=20°时，∠EDC=
 
°；
（2）当DC等于多少时△ABD≌△DCE？并说明理由；
（3）在点D的运动过程中，△ADE的形状也在改变，判断当∠BAD等于多少度时，△ADE是等腰三角形．
符号“f”表示一种运算，它对一些数的运算结果如下：
（1）f（1）=0，f（2）=1，f（3）=2，f（4）=3，…
（2）f（
1
2
）=-2，f（
1
3
）=-3，f（
1
4
）=-4，f（
1
5
）=-5，…
利用以上规律计算f（
1
2010
）+f（2010）=
 
．
如图，已知圆的半径为r，求外接正六边形的边长．
一个矩形的对角线长为6，对角线与一边的夹角为45°，则这个矩形周长为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网