题目内容
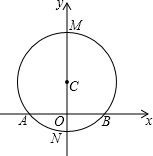 如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,以直线AB为x轴,直线MN为y轴建立坐标系.我们把横纵坐标都是整数的点叫做整数点,请写出⊙C上位于第二象限和第三象限的整数点的坐标
如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,以直线AB为x轴,直线MN为y轴建立坐标系.我们把横纵坐标都是整数的点叫做整数点,请写出⊙C上位于第二象限和第三象限的整数点的坐标考点:垂径定理,坐标与图形性质,勾股定理
专题:计算题
分析:连结AC,如图,作半径CD⊥y轴,根据垂径定理得AO=
AB=4,在Rt△AOC中根据勾股定理计算出OC=3,则C点坐标为(0,3),D点坐标为(-5,3),N点坐标为(-2,0),M点坐标为(8,0),然后分类讨论:由于⊙C上位于第二象限和第三象限的整数点的横坐标只能为-1、-2、-3、-4、-5,则设出整数点的坐标,利用两点间的距离公式建立关于整数点的纵坐标的方程,再解方程确定满足条件的纵坐标即可.
| 1 |
| 2 |
解答:解: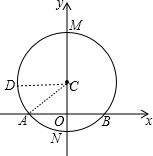 连结AC,如图,作半径CD⊥y轴,
连结AC,如图,作半径CD⊥y轴,
∵直径MN=10,
∴AC=CM=CN=CD=5,
∵MN⊥AB,
∴AO=BO=
AB=4,
在Rt△AOC中,OC=
=3,
∴C点坐标为(0,3),D点坐标为(-5,3),
∴N点坐标为(-2,0),M点坐标为(8,0),
当⊙C上位于第二象限和第三象限的整数点的坐标为(-1,t),则12+(t-3)2=52,解得t1=3+2
,t2=3-2
,t的值不是整数,舍去;
当⊙C上位于第二象限和第三象限的整数点的坐标为(-2,t),则(-2)2+(t-3)2=52,解得t1=3+
,t2=3-
,t的值不是整数,舍去;
当⊙C上位于第二象限和第三象限的整数点的坐标为(-3,t),则(-3)2+(t-3)2=52,解得t1=-1,t2=7,满足条件的整数点的坐标为(-3,-1),(-3,7);
当⊙C上位于第二象限和第三象限的整数点的坐标为(-4,t),则(-4)2+(t-3)2=52,解得t1=0(舍去),t2=6,满足条件的整数点的坐标为(-4,6);
当⊙C上位于第二象限和第三象限的整数点的坐标为(-5,t),则(-5)2+(t-3)2=52,解得t1=t2=3,满足条件的整数点的坐标为(-5,3),
∴⊙C上位于第二象限和第三象限的整数点的坐标为(-3,-1),(-3,7),(-4,6),(-5,3).
故答案为(-3,-1),(-3,7),(-4,6),(-5,3).
 连结AC,如图,作半径CD⊥y轴,
连结AC,如图,作半径CD⊥y轴,∵直径MN=10,
∴AC=CM=CN=CD=5,
∵MN⊥AB,
∴AO=BO=
| 1 |
| 2 |
在Rt△AOC中,OC=
| AC2-AO2 |
∴C点坐标为(0,3),D点坐标为(-5,3),
∴N点坐标为(-2,0),M点坐标为(8,0),
当⊙C上位于第二象限和第三象限的整数点的坐标为(-1,t),则12+(t-3)2=52,解得t1=3+2
| 6 |
| 6 |
当⊙C上位于第二象限和第三象限的整数点的坐标为(-2,t),则(-2)2+(t-3)2=52,解得t1=3+
| 21 |
| 21 |
当⊙C上位于第二象限和第三象限的整数点的坐标为(-3,t),则(-3)2+(t-3)2=52,解得t1=-1,t2=7,满足条件的整数点的坐标为(-3,-1),(-3,7);
当⊙C上位于第二象限和第三象限的整数点的坐标为(-4,t),则(-4)2+(t-3)2=52,解得t1=0(舍去),t2=6,满足条件的整数点的坐标为(-4,6);
当⊙C上位于第二象限和第三象限的整数点的坐标为(-5,t),则(-5)2+(t-3)2=52,解得t1=t2=3,满足条件的整数点的坐标为(-5,3),
∴⊙C上位于第二象限和第三象限的整数点的坐标为(-3,-1),(-3,7),(-4,6),(-5,3).
故答案为(-3,-1),(-3,7),(-4,6),(-5,3).
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理、两点间的距离公式和坐标与图形性质.

练习册系列答案
相关题目
 如图,已知二次函数y=-
如图,已知二次函数y=- 如图,四边形ABCD是一个长方形的台球桌,台球桌上还剩一个黑球没有被打进球袋,在点P的位置,现在轮到你打,你应该把在点Q位置的白球打到AB边上的哪一个点,才能反弹回来撞到黑球?试作图说明.
如图,四边形ABCD是一个长方形的台球桌,台球桌上还剩一个黑球没有被打进球袋,在点P的位置,现在轮到你打,你应该把在点Q位置的白球打到AB边上的哪一个点,才能反弹回来撞到黑球?试作图说明. 若∠ADE=∠B,AD=6,AB=12,DE=5,则BC的长为
若∠ADE=∠B,AD=6,AB=12,DE=5,则BC的长为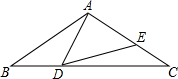 如图,△ABC中,AB=AC=2,∠B=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
如图,△ABC中,AB=AC=2,∠B=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.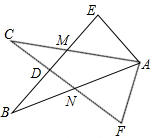 如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△ACN≌△ABM.其中正确的结论是
如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△ACN≌△ABM.其中正确的结论是
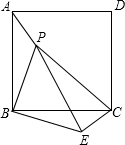 如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转与△CBE重合,若PB=3,则PE=
如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转与△CBE重合,若PB=3,则PE=