题目内容
某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=-x+120
(1)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少?
(2)销售单价定为多少元时,该商场获得的利润恰为500元?
(1)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少?
(2)销售单价定为多少元时,该商场获得的利润恰为500元?
考点:二次函数的应用
专题:
分析:(1)依题意求出W与x的函数表达式.将二次函数的解析式配方后即可确定最值;
(2)由w=500推出x2-180x+7200=0,解出x的值即可.
(2)由w=500推出x2-180x+7200=0,解出x的值即可.
解答:解:(1)由题意知
W=(x-60)•(-x+120)
=-x2+180x-7200
=-(x-90)2+900,
∵抛物线的开口向下,
∴当x<90时,W随x的增大而增大,而销售单价不低于成本单价,且获利不得高于45%,
即x-60≤60×45%,
∴60≤x≤87,
∴当x=87时,W=-(87-90)2+900=891.
答:当销售单价定为87元时,商场可获得最大利润,最大利润是891元;
(2)如果在试销期间该服装部想要获得500元的利润,∴500=-x2+180x-7200,
解为 x1=70,x2=110(不合题意舍去).
∴销售单价应定为70元.
答:销售单价定为70元时,该商场获得的利润恰为500元.
W=(x-60)•(-x+120)
=-x2+180x-7200
=-(x-90)2+900,
∵抛物线的开口向下,
∴当x<90时,W随x的增大而增大,而销售单价不低于成本单价,且获利不得高于45%,
即x-60≤60×45%,
∴60≤x≤87,
∴当x=87时,W=-(87-90)2+900=891.
答:当销售单价定为87元时,商场可获得最大利润,最大利润是891元;
(2)如果在试销期间该服装部想要获得500元的利润,∴500=-x2+180x-7200,
解为 x1=70,x2=110(不合题意舍去).
∴销售单价应定为70元.
答:销售单价定为70元时,该商场获得的利润恰为500元.
点评:此题主要考查了二次函数的应用,利用二次函数解决实际问题是初中阶段重点题型,同学们应重点掌握.

练习册系列答案
相关题目
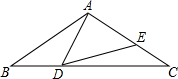 如图,△ABC中,AB=AC=2,∠B=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
如图,△ABC中,AB=AC=2,∠B=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.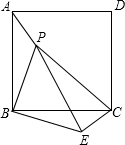 如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转与△CBE重合,若PB=3,则PE=
如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转与△CBE重合,若PB=3,则PE=