Question

4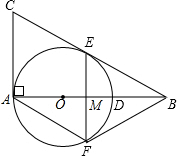．如图，在Rt△ABC中，∠BAC=90°，O是AB边上的一点，以OA为半径的⊙O与边AB相交于点D，与边BC相切于点E．
（1）若AC=6，BC=10，求⊙O的半径．
（2）过点E作弦EF⊥AB于M，连接AF，若AD=4，∠AFE=60°，
①求劣弧EF的长．②求弦EF的长，并说明四边形ACEF是什么特殊四边形？

Answer 1

分析 （1）连接OE，设圆的半径为r，在直角三角形ABC中，利用勾股定理求出AB的长，根据BC与圆相切，得到OE垂直于BC，进而得到一对直角相等，再由一对公共角，利用两角相等的三角形相似得到三角形BOE与三角形ABC相似，由相似得比例求出r的值即可；
（2）①求出∠EOF=120°，由弧长公式即可得出结果；
②由垂径定理得出EM=FM，由勾股定理求出EM，即可得出EF的长；证出CA∥EF，CB∥AF，得出四边形ACEF为平行四边形，再由∠CAB为直角，得到CA为圆的切线，利用切线长定理得到CA=CE，利用邻边相等的平行四边形为菱形即可得证．

解答 解：（1）连接OE，如图1所示：
设圆O半径为r，
在Rt△ABC中，BC=10，AC=6，
根据勾股定理得：AB=$\sqrt{B{C}^{2}-A{C}^{2}}$=8，
∵BC与圆O相切，
∴OE⊥BC，
∴∠OEB=∠BAC=90°，
∵∠B=∠B，
∴△BOE∽△BCA，
∴$\frac{OE}{AC}=\frac{BO}{BC}$，即$\frac{r}{6}=\frac{8-r}{10}$，
解得：r=3；
（2）①连接OF，如图2所示：
∵EF⊥AB，
∴EM=FM，$\widehat{DE}=\widehat{DF}$，
∴∠EOD=∠FOD，
∵∠AOE=2∠AFE=120°，
∴∠EOD=60°，
∴∠EOF=120°，
∵AD=4，∴OE=OA=2，
∴劣弧EF的长=$\frac{120π×{2}^{2}}{360}$=$\frac{4}{3}π$；
②∵EF⊥AB，∠EOD=60°，
∴∠OEM=30°，
∴OM=$\frac{1}{2}$OE=1，
∴EM=$\sqrt{3}$OM=$\sqrt{3}$，
∴EF=2EM=2$\sqrt{3}$；
四边形ACEF是菱形；理由如下：
∵EF⊥AB，
∴∠EMB=∠CAB=90°，
∴∠MEB=∠F=60°，CA∥EF，
∴CB∥AF，
∴四边形ACEF为平行四边形，
∵∠CAB=90°，OA为半径，
∴CA为圆O的切线，
∵BC为圆O的切线，
∴CA=CE，
∴平行四边形ACEF为菱形．

点评 此题考查了切线的性质，菱形的判定，相似三角形的判定与性质，勾股定理，以及垂径定理，熟练掌握有关性质及定理是解本题的关键．