题目内容
17. 如图,在△ABC中,∠ACB=90°,分别以点A,B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点M,N,作直线MN分别交AB,AC于点D,E,连结CD,BE,下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A,B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点M,N,作直线MN分别交AB,AC于点D,E,连结CD,BE,下列结论错误的是( )| A. | AD=CD | B. | BE>CD | C. | ∠BEC=∠BDC | D. | BE平分∠CBD |
分析 根据题意可知DE是AB的垂直平分线,由此即可得出△AEB是等腰三角形,由Rt△ABC中点D是AB的中点,可得△ACD和△BCD均为等腰三角形,据此作出判断.
解答  解:由题可得,DE是AB的垂直平分线,
解:由题可得,DE是AB的垂直平分线,
∴AE=BE,AD=BD,故A选项正确;
∵Rt△ABC中,点D是AB的中点,
∴CD=AD,
∵DE⊥AB,
∴Rt△ADE中,AE>AD,
∴BE>CD,故B选项正确;
∵∠BEC是等腰△ABE的外角,
∴∠BEC=2∠A,
∵∠BDC是等腰△ACD的外角,
∴∠BDC=2∠A,
∴∠BEC=∠BDC,故C选项正确;
∵当∠A=30°时,∠ABE=30°=∠CBE,
∴当∠A=30°时,BE平分∠ABC,
而∠A不一定为30°,
∴BE不一定平分∠CBD,故D选项错误.
故选:D.
点评 本题考查了线段的垂直平分线的性质、等腰三角形的性质,直角三角形斜边上中线的性质等知识的运用,解题时注意:在直角三角形中,斜边上的中线等于斜边的一半;线段垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
5.某种商品零售价经过两次降价后,价格为降价前的64%,则平均每次降价( )
| A. | 10% | B. | 19% | C. | 9.5% | D. | 20% |
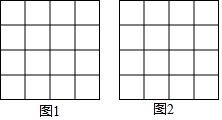 如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,请你以格点为顶点分别在图1和图2中画一个直角三角形,使它的三边长都是无理数.(两个三角形不全等)
如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,请你以格点为顶点分别在图1和图2中画一个直角三角形,使它的三边长都是无理数.(两个三角形不全等) 如图,?ABCD的对角线AC和BD相交于点O,那么图中的全等三角形共有4对.
如图,?ABCD的对角线AC和BD相交于点O,那么图中的全等三角形共有4对.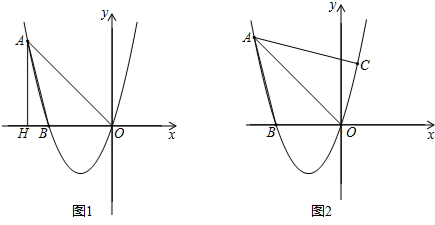
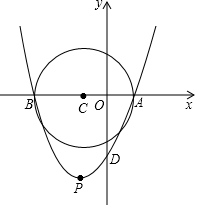 如图,已知⊙C的圆心在x轴上,且进过A(1,0),B(-3,0)两点,抛物线y=ax2+bx+c(a>0)经过A、B两点,顶点为P.
如图,已知⊙C的圆心在x轴上,且进过A(1,0),B(-3,0)两点,抛物线y=ax2+bx+c(a>0)经过A、B两点,顶点为P.