题目内容
14.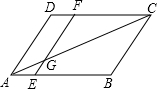 在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )
在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
分析 根据平行四边形定义得AD∥BC,由已知的EF∥AD得BC∥FE,根据平行相似得比例式:$\frac{AE}{AB}=\frac{AG}{AC}$,代入可求出AG的长.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵AD∥EF,
∴EF∥BC,
∴△AEG∽△ABC,
∴$\frac{AE}{AB}=\frac{AG}{AC}$,
∵AE=1,BE=3,AC=6,
∴$\frac{1}{1+3}=\frac{AG}{6}$,
∴AG=1.5,
故选B.
点评 本题考查了平行四边形的性质和相似三角形的性质和判定,同时还要知道:如果两条直线都与第三条直线平行,那么这两条直线也互相平行;在几何推理中,常利用平行线分线段成比例定理或相似列比例式求线段的长,因此要熟练掌握相似的判定方法:①平行相似,②两角法,③三边法,④两边及夹角法.

练习册系列答案
相关题目
 如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠BFE=67.5°,AE=2.
如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠BFE=67.5°,AE=2.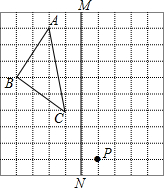 如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)
如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上) 如图,由边长为1的25个小正方形组成的正方形网格中有一个△ABC,请在网格中画一个顶点在小正方形的格点上,且与△ABC相似的面积最大的△A'B'C',并求出它的面积S.
如图,由边长为1的25个小正方形组成的正方形网格中有一个△ABC,请在网格中画一个顶点在小正方形的格点上,且与△ABC相似的面积最大的△A'B'C',并求出它的面积S. 如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处.
如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处. 有一个高为1.5m,半径是1m的圆柱形油桶,在靠近边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5m,问这根铁棒有多长?
有一个高为1.5m,半径是1m的圆柱形油桶,在靠近边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5m,问这根铁棒有多长? 如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,∠FDE=65°,则∠A=50°.
如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,∠FDE=65°,则∠A=50°. 如图,∠C=36°,∠B=72°,∠BAD=36°,找出图中所有的等腰三角形△ABD,△ABC,△ADC.
如图,∠C=36°,∠B=72°,∠BAD=36°,找出图中所有的等腰三角形△ABD,△ABC,△ADC.