题目内容
3. 如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,∠FDE=65°,则∠A=50°.
如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,∠FDE=65°,则∠A=50°.
分析 由条件可证明△BDF≌△CED,再利用外角的性质可求得∠B=∠FDE,在△ABC中利用三角形内角和定理可求得∠A.
解答 解:
在△BDF和△CED中
$\left\{\begin{array}{l}{BF=CD}\\{∠B=∠C}\\{BD=CE}\end{array}\right.$
∴△BDF≌△CED(SAS),
∴∠BFD=∠CDE,
∵∠FDE+∠FDC=∠B+∠BFD,
∴∠B=∠FDE=65°,
∴∠A=180°-∠B-∠C=180°-65°-65°=50°,
故答案为:50.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应角相等、对应边相等)是解题的关键.

练习册系列答案
相关题目
14.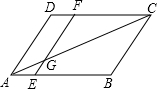 在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )
在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )
 在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )
在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
18.解方程x2+2016x=0的最佳方案是( )
| A. | 配方法 | B. | 直接开平方法 | C. | 公式法 | D. | 因式分解法 |
12.把(-5)+(-3)+(+1)+(-16)写成省略括号和加号的形式是( )
| A. | -5+3+1-16 | B. | -5-3+1-16 | C. | -5-3-1+16 | D. | -5+3+1+16 |
 如图,在△ABC中,点D、E分别在AB、AC 边上,AB=AC,BE=BC,AE=DE=DB,那么∠A=45度.
如图,在△ABC中,点D、E分别在AB、AC 边上,AB=AC,BE=BC,AE=DE=DB,那么∠A=45度.