题目内容
4. 如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠BFE=67.5°,AE=2.
如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠BFE=67.5°,AE=2.(1)求∠AEB的度数;
(2)求长方形纸片ABCD的纸片的面积.
分析 (1)由AD∥BC与折叠的性质,可求得∠BEF=∠DEF=∠BFE=67.5°,继而求得答案;
(2)首先由直角三角形的性质,可求得∠ABE=∠AEB=45°,即可得AB=AE=2,然后由勾股定理求得BE的长,继而求得AD的长,则可求得答案.
解答 解:(1)∵AD∥BC,
∴∠DEF=∠BFE=67.5°;
又∵∠BEF=∠DEF=67.5°,
∴∠AEB=180°-∠BEF-∠DEF=180°-67.5°-67.5°=45°;
(2)在直角△ABE中,由(1)知∠AEB=45°,
∴∠ABE=90°-∠AEB=90°-45°=45°,
∴AB=AE=2,
∴BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
又∵AD=AE+DE=AE+BE=2+2$\sqrt{2}$,
∴长方形纸片ABCD的面积为:AB×AD=2×(2+2$\sqrt{2}$)=4+4$\sqrt{2}$.
点评 此题考查了折叠的性质、矩形的性质、勾股定理以及等腰三角形的判定与性质.注意掌握折叠前后图形的对应关系.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
9.若关于x的方程kx2-(k+1)x+1=0的根是整数,则满足条件的整数k的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.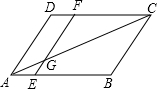 在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )
在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )
 在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )
在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |

 如图,已知点A,D,B在同一直线上,∠1=∠2,∠3=∠E,若∠DAE=100°,∠E=30°,求∠B的度数.
如图,已知点A,D,B在同一直线上,∠1=∠2,∠3=∠E,若∠DAE=100°,∠E=30°,求∠B的度数.