题目内容
4. 如图,∠C=36°,∠B=72°,∠BAD=36°,找出图中所有的等腰三角形△ABD,△ABC,△ADC.
如图,∠C=36°,∠B=72°,∠BAD=36°,找出图中所有的等腰三角形△ABD,△ABC,△ADC.
分析 根据三角形的内角和等于180°求出∠CAD=36°,∠ADB=72°,从而求出∠C=∠CAD,∠B=∠ADB,根据等角对等边可得AD=CD,AD=AB,再求出∠CAB=∠B,根据等角对等边求出AC=BC,然后根据等腰三角形的定义写出等腰三角形即可.
解答 解:∵∠C=36°,∠B=72°,∠BAD=36°,
∴∠CAD=180°-∠C-∠B-∠BAD=180°-36°-72°-36°=36°,
∠ADB=180°-∠B-∠BAD=180°-72°-36°=72°,
∴∠C=∠CAD,∠B=∠ADB,
∴AD=CD,AD=AB,
∴△ABD和△ADC是等腰三角形,
∵∠CAB=∠CAD+∠BAD=36°+36°=72°,
∴∠CAB=∠B,
∴AC=BC,
∴△ABC是等腰三角形,
∴等腰三角形有:△ABD,△ABC,△ADC.
故答案为:△ABD,△ABC,△ADC.
点评 本题考查了等腰三角形的判定,三角形内角和定理,利用角的度数相等得到相等的角是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
14.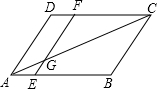 在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )
在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )
 在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )
在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
12.把(-5)+(-3)+(+1)+(-16)写成省略括号和加号的形式是( )
| A. | -5+3+1-16 | B. | -5-3+1-16 | C. | -5-3-1+16 | D. | -5+3+1+16 |
9.向东行进-50m表示的意义是( )
| A. | 向东行进50 m | B. | 向南行进50 m | C. | 向北行进50 m | D. | 向西行进50 m |

 如果,BO是Rt△ABC斜边上的中线,延长BO到点D,使DO=BO,连接AD,CD.四边形ABCD是矩形吗?请说明理由.
如果,BO是Rt△ABC斜边上的中线,延长BO到点D,使DO=BO,连接AD,CD.四边形ABCD是矩形吗?请说明理由. 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M为AC的中点,过点M作MN∥AD交CD于点 N,连接BM,BN.
如图,在四边形ABCD中,∠ABC=90°,AC=AD,M为AC的中点,过点M作MN∥AD交CD于点 N,连接BM,BN.