题目内容
19. 如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处.
如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处.(1)求A、B两点的坐标;
(2)求S△ABO.
(3)求点O到直线AB的距离.
(4)求直线AM的解析式.
分析 (1)由解析式令x=0,y=-$\frac{4}{3}$x+8=8,即B(0,8),令y=0时,x=6,即A(6,0);
(2)根据三角形面积公式即可求得;
(3)根据三角形面积求得即可;
(4)由折叠的性质,可求得AB′与OB′的长,BM=B′M,然后设MO=x,由在Rt△OMB′中,OM2+OB′2=B′M2,求出M的坐标,设直线AM的解析式为y=kx+b,再把A、M坐标代入就能求出解析式.
解答 解:(1)当x=0时,y=-$\frac{4}{3}$x+8=8,即B(0,8),
当y=0时,x=6,即A(6,0);
(2)∵点A的坐标为:(6,0),点B坐标为:(0,8),∠AOB=90°,
∴OA=6,OB=8,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=10,
∴S△ABO.=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×6×8=24;
(3)设点O到直线AB的距离为h,
∵S△ABO=$\frac{1}{2}$OA•OB=$\frac{1}{2}$AB•h,
∴$\frac{1}{2}$×6×8=$\frac{1}{2}$×10h,
解得h=4.8,
∴点O到直线AB的距离无4.8;
(4)由折叠的性质,得:AB=AB′=10,
∴OB′=AB′-OA=10-6=4,
设MO=x,则MB=MB′=8-x,
在Rt△OMB′中,OM2+OB′2=B′M2,
即x2+42=(8-x)2,
解得:x=3,
∴M(0,3),
设直线AM的解析式为y=kx+b,把(0,3);(6,0),
代入可得y=-$\frac{1}{2}$x+3.
点评 此题考查了折叠的性质、待定系数法求一次函数的解析式、一次函数图象上点的坐标特征、勾股定理等知识,解答本题的关键是求出OM的长度.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 当d=8cm时,直线与圆相交 | B. | 当d=4.5cm时,直线与圆相离 | ||
| C. | 当d=6.5cm时,直线与圆相切 | D. | 当d=13cm时,直线与圆相切 |
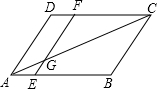 在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )
在?ABCD中,EF∥AD,EF交AC于点G,若AE=1,BE=3,AC=6,AG的长为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
| A. | 向东行进50 m | B. | 向南行进50 m | C. | 向北行进50 m | D. | 向西行进50 m |
 如图,AB是⊙O的直径,弦CD与AB相交于点P,∠AOD=70°,∠APD=60°.求∠BDC的度数.
如图,AB是⊙O的直径,弦CD与AB相交于点P,∠AOD=70°,∠APD=60°.求∠BDC的度数. 如图,在△ABC中,点D、E分别在AB、AC 边上,AB=AC,BE=BC,AE=DE=DB,那么∠A=45度.
如图,在△ABC中,点D、E分别在AB、AC 边上,AB=AC,BE=BC,AE=DE=DB,那么∠A=45度.