题目内容
20.已知,△ABC的三边为a、b、c,且∠B=60°,sinA×sinC=$\frac{1}{4}$,若S△ABC=$\sqrt{3}$,则b=2$\sqrt{3}$.分析 首先利用三角形的面积公式求得a=$\frac{4}{c}$,由于sinA×sinC=$\frac{1}{4}$,得到sinA=$\frac{1}{4sinC}$,再根据正弦定理得到$\frac{b}{sinB}$=$\frac{c}{sibC}$=4,于是求出结果.
解答 解:∵S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}$ac•$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴ac=4,
∴a=$\frac{4}{c}$,
∵sinA×sinC=$\frac{1}{4}$,
∴sinA=$\frac{1}{4sinC}$,
由正弦定理得:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$,
∴$\frac{\frac{4}{c}}{\frac{1}{4sinC}}$=$\frac{c}{sinC}$,
∴$\frac{16sinC}{c}=\frac{c}{sinC}$,
∴$\frac{{c}^{2}}{si{n}^{2}C}=16$,
∴$\frac{c}{sinC}$=4,
∴$\frac{b}{sinB}$=4,
∴$\frac{b}{sin60°}=4$,
∴$b=2\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查了三角形的面积公式,正弦定理,本题有一定的难度,熟练掌握正弦定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,再直爬向C点停止,已知点A表示-$\sqrt{2}$,点C表示2,设点B所表示的数为m.
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,再直爬向C点停止,已知点A表示-$\sqrt{2}$,点C表示2,设点B所表示的数为m. 如图,已知AF=BE,∠A=∠B,AC=BD,求证:∠F=∠E.
如图,已知AF=BE,∠A=∠B,AC=BD,求证:∠F=∠E.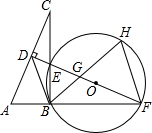 如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相较于点D,E,F,且BF=BC,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相较于点D,E,F,且BF=BC,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.