Question

12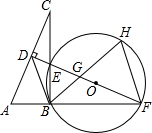．如图，在Rt△ABC中，∠ABC=90°，AC的垂直平分线分别与AC，BC及AB的延长线相较于点D，E，F，且BF=BC，⊙O是△BEF的外接圆，∠EBF的平分线交EF于点G，交⊙O于点H，连接BD，FH．
（1）求证：△ABC≌△EBF；
（2）试判断BD与⊙O的位置关系，并说明理由；
（3）若AB=1，求HG•HB的值．

Answer 1

分析 （1）由垂直的定义可得∠EBF=∠ADF=90°，于是得到∠C=∠BFE，从而证得△ABC≌△EBF；
（2）BD与⊙O相切，如图1，连接OB证得∠DBO=90°，即可得到BD与⊙O相切；
（3）如图2，连接CF，HE，有等腰直角三角形的性质得到CF=$\sqrt{2}$BF，由于DF垂直平分AC，得到AF=CF=AB+BF=1+BF=$\sqrt{2}$BF，求得BF=$\sqrt{2}+1$，有勾股定理解出EF$\sqrt{{BF}^{2}+B{E}^{2}}$=$\sqrt{4+2\sqrt{2}}$，推出△EHF是等腰直角三角形，求得HF=$\frac{\sqrt{2}}{2}$EF=$\sqrt{2+\sqrt{2}}$，通过△BHF∽△FHG，列比例式即可得到结论．

解答 （1）证明：∵∠ABC=90°，
∴∠EBF=90°，
∵DF⊥AC，
∴∠ADF=90°，
∴∠C+∠A=∠A+∠AFD=90°，
∴∠C=∠BFE，
在△ABC与△EBF中，$\left\{\begin{array}{l}{∠C=∠AFE}\\{BC=BF}\\{∠ABC=∠EBF}\end{array}\right.$，
∴△ABC≌△EBF；

（2）BD与⊙O相切，如图1，连接OB
证明如下：∵OB=OF，
∴∠OBF=∠OFB，
∵∠ABC=90°，AD=CD，
∴BD=CD，
∴∠C=∠DBC，
∵∠C=∠BFE，
∴∠DBC=∠OBF，
∵∠CBO+∠OBF=90°，∴∠DBC+∠CBO=90°，
∴∠DBO=90°，
∴BD与⊙O相切；

（3）解：如图2，连接CF，HE，
∵∠CBF=90°，BC=BF，
∴CF=$\sqrt{2}$BF，
∵DF垂直平分AC，
∴AF=CF=AB+BF=1+BF=$\sqrt{2}$BF，
∴BF=$\sqrt{2}+1$，
∵△ABC≌△EBF，
∴BE=AB=1，
∴EF=$\sqrt{{BF}^{2}+B{E}^{2}}$=$\sqrt{4+2\sqrt{2}}$，
∵BH平分∠CBF，
∴$\widehat{EH}=\widehat{HF}$，
∴EH=FH，
∴△EHF是等腰直角三角形，
∴HF=$\frac{\sqrt{2}}{2}$EF=$\sqrt{2+\sqrt{2}}$，
∵∠EFH=∠HBF=45°，∠BHF=∠BHF，
∴△BHF∽△FHG，
∴$\frac{HF}{HG}=\frac{BH}{HF}$，
∴HG•HB=HF²=2+$\sqrt{2}$．

点评 本题考查了全等三角形的判定和性质，相似三角形的判定和性质，圆周角定理，勾股定理，线段的垂直平分线的性质，直角三角形的性质，等腰直角三角形的判定和性质，熟练掌握这些定理是解题的关键．