题目内容
19.设方程x2-8x+4=0的两根分别是x1、x2,不解方程试求下列各式的值.(1)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$;
(2)${{x}_{1}}^{2}$+${{x}_{2}}^{2}$;
(3)$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$.
分析 (1)根据韦达定理可得x1+x2=8,x1x2=4,代入$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$计算可得;
(2)将x1+x2、x1x2代入${{x}_{1}}^{2}$+${{x}_{2}}^{2}$=(x1+x2)2-2x1x2可得;
(3)将x1+x2、x1x2代入$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$即可得.
解答 解:(1)∵方程x2-8x+4=0的两根分别是x1、x2,
∴x1+x2=8,x1x2=4,
则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{8}{4}$=2;
(2)${{x}_{1}}^{2}$+${{x}_{2}}^{2}$=(x1+x2)2-2x1x2=64-8=56;
(3)$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{{8}^{2}-2×4}{4}$=14.
点评 本题主要考查根与系数的关系,掌握韦达定理是解题的根本,将待求代数式灵活变形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.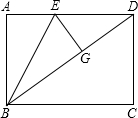 如图,矩形ABCD,AB=3,BC=4,点E是AD上一点,连接BE,将△ABE沿BE折叠,点A恰好落在BD上的点G处,则AE的长为( )
如图,矩形ABCD,AB=3,BC=4,点E是AD上一点,连接BE,将△ABE沿BE折叠,点A恰好落在BD上的点G处,则AE的长为( )
 如图,矩形ABCD,AB=3,BC=4,点E是AD上一点,连接BE,将△ABE沿BE折叠,点A恰好落在BD上的点G处,则AE的长为( )
如图,矩形ABCD,AB=3,BC=4,点E是AD上一点,连接BE,将△ABE沿BE折叠,点A恰好落在BD上的点G处,则AE的长为( )| A. | 2 | B. | $\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
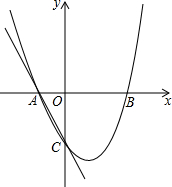 如图,一次函数y=x2-x-2的图象交x轴于A,B两点,交y轴于C,点M在第一象限的抛物线上,CM交x轴于点P,且PA=PC,求点M的坐标.
如图,一次函数y=x2-x-2的图象交x轴于A,B两点,交y轴于C,点M在第一象限的抛物线上,CM交x轴于点P,且PA=PC,求点M的坐标. 把一块直尺与一块三角板如图放置,若∠1=39°,则∠2的度数为129°.
把一块直尺与一块三角板如图放置,若∠1=39°,则∠2的度数为129°.