题目内容
8．
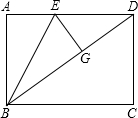如图，矩形ABCD，AB=3，BC=4，点E是AD上一点，连接BE，将△ABE沿BE折叠，点A恰好落在BD上的点G处，则AE的长为（ ）| A． | 2 | B． | $\frac{5}{2}$ | C． | $\frac{3}{2}$ | D． | 3 |
分析 先用勾股定理求出BD，再由折叠得出BG=AB=3，从而求出DG=2，最后再用勾股定理求解即可．
解答 解：在Rt△ABD中，AB=3，AD=BC=4，
∴BD=5
由折叠得，∠BEG=∠A=90°，BG=AB=3，EG=AE，
∴DG=BD-BG=2，DE=AD-AE=4-AE，
在Rt△DEG中，EG2+DG2=DE2，
∴AE2+4=（4-AE）2，
∴AE=$\frac{3}{2}$，
故选C．
点评 本题考查了翻折变换的性质，勾股定理，此类题目熟记性质并利用勾股定理列出方程是解题的关键．
练习册系列答案
相关题目
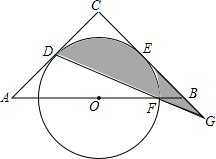如图，已知△ABC，AC=BC=6，∠C=90°，O是AB的中点，⊙O与AC相切于点D，与BC相切于点E．⊙O交OB于F，连接DF并延长交CB的延长线于G．
16．投掷一枚均匀的骰子，掷出的点数是3的倍数的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
