题目内容
18.在Rt△ABC中,∠C=90°,AC=3,BC=4,则点C到AB的距离是( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{3}{4}$ |
分析 首先根据勾股定理求出斜边AB的长,再根据三角形的面积为定值即可求出则点C到AB的距离.
解答  解:在Rt△ABC中,∠C=90°,则有AC2+BC2=AB2,
解:在Rt△ABC中,∠C=90°,则有AC2+BC2=AB2,
∵BC=4,AC=3,
∴AB=5,
设AB边上的高为h,
则S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•h,
∴h=$\frac{12}{5}$,
故选:C.
点评 本题考查了勾股定理在直角三角形中的应用,解本题的关键是正确的运用勾股定理,确定AB为斜边.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
6.已知(-1,y1),(-2,y2),(-4,y3)是抛物线y=-2(x+2)2+m上的点,则( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y2>y1>y3 | D. | y2>y3>y1 |
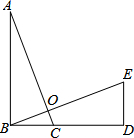 如图,△ABC≌△BDE,点B、C、D在一条直线上,AC、BE交于点O,若∠AOE=95°,则∠BDE=95°.
如图,△ABC≌△BDE,点B、C、D在一条直线上,AC、BE交于点O,若∠AOE=95°,则∠BDE=95°. 如图,在△ABC中,BC的垂直平分线分别交AB、BC于D、E,若△ACD的周长为10cm,AC=3cm,则AB=7 cm.
如图,在△ABC中,BC的垂直平分线分别交AB、BC于D、E,若△ACD的周长为10cm,AC=3cm,则AB=7 cm. 如图,BD∥CE,∠1=85°,∠2=37°,则∠A=48°.
如图,BD∥CE,∠1=85°,∠2=37°,则∠A=48°. 如图,在阳光下某一时刻大树AB的影子落在墙DE上的C点,同时1.2m的标杆影长3m,已知CD=4m,BD=6m,求大树的高度.
如图,在阳光下某一时刻大树AB的影子落在墙DE上的C点,同时1.2m的标杆影长3m,已知CD=4m,BD=6m,求大树的高度. 判断满足下列关系的两个三角形是否是位似图形?如果是,请指出位似中心.
判断满足下列关系的两个三角形是否是位似图形?如果是,请指出位似中心.