题目内容
3. 如图,BD∥CE,∠1=85°,∠2=37°,则∠A=48°.
如图,BD∥CE,∠1=85°,∠2=37°,则∠A=48°.
分析 根据平行线的性质求得∠BDC=∠1=85°,结合三角形外角性质来求∠A的度数即可.
解答 解:∵BD∥CE,∠1=85°,
∴∠BDC=∠1=85°,
又∵∠BDC=∠2+∠A,∠2=37°,
∴∠A=85°-37°=48°.
故答案是:48.
点评 本题考查了平行线的性质和三角形的外角性质.解题的关键是找出内错角相等.

练习册系列答案
相关题目
11.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.在Rt△ABC中,∠C=90°,AC=3,BC=4,则点C到AB的距离是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{3}{4}$ |
8. 如图,正方形ABCD的边长为2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图,正方形ABCD的边长为2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
 如图,正方形ABCD的边长为2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图,正方形ABCD的边长为2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{6}$ |
12.下列根式中,属于最简二次根式的是( )
| A. | $\sqrt{30}$ | B. | $\sqrt{18}$ | C. | $\sqrt{9}$ | D. | $\sqrt{\frac{1}{3}}$ |
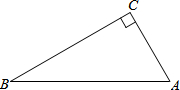 如图,在△ABC中,∠C=90°,∠A>∠B.
如图,在△ABC中,∠C=90°,∠A>∠B. 如图,AB=AC,∠A=36°,BD是∠ABC的角平分线,求证:△ABC∽△BCD.
如图,AB=AC,∠A=36°,BD是∠ABC的角平分线,求证:△ABC∽△BCD.