题目内容
6.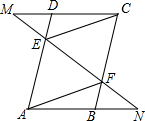 如图,已知在平行四边形ABCD中,E、F分别是边AD、BC上的点,且DE=BF,过E、F两点作直线,分别与CD、AB的延长线相交于点M、N,连接CE、AF.
如图,已知在平行四边形ABCD中,E、F分别是边AD、BC上的点,且DE=BF,过E、F两点作直线,分别与CD、AB的延长线相交于点M、N,连接CE、AF.求证:(1)四边形AFCE是平行四边形;
(2)△MEC≌△NFA.
分析 (1)由平行四边形的性质可证得AE=CF且AE∥CF,可证得结论;
(2)由(1)结合平行四边形的性质可得到EC=AF,∠ECF=∠EAF,可证∠MCE=∠NAF,则可证明△MEC≌△NFA.
解答 证明:
(1)∵四边形ABCD是平行四边形,
∴AD∥BC且 AD=BC,
又∵DE=BF,
∴AE=CF,
∴四边形AFCE是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴∠MCB=∠NAD,且CD∥AB,
∴∠M=∠N,
∵四边形AFCE是平行四边形,
∴EC=AF,∠ECF=∠EAF,
∴∠MCE=∠NAF,
在△MEC和△NFA中
$\left\{\begin{array}{l}{∠MCE=∠NFA}\\{∠M=∠N}\\{EC=AF}\end{array}\right.$
∴△MEC≌△NFA(AAS).
点评 本题主要考查平行四边形的性质和判定,掌握平行四边形的对边平行且相等、对角相等和对角线互相平分是解题的关键.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | 顺次连接矩形各边中点的四边形一定也是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 有一个角是直角的菱形一定是正方形 | |
| D. | 平行四边形的对角线相等且互相平分 |
18.甲、乙两数和为21,甲数的2倍等于乙数的5倍,求甲、乙两数.设甲数为x,乙数为y,则下列方程组正确的是( )
| A. | $\left\{{\begin{array}{l}x+y=21\\ 5x=2y\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}x+y=21\\ 2x=5y\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}2x+5y=21\\ 2x=5y\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}2x+5y=21\\ 5x=2y\end{array}}\right.$ |
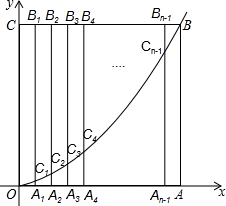 如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,当B25C25=8C25A25时,则n=75.
如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,当B25C25=8C25A25时,则n=75. 平行四边形ABCD中,AB=3cm,∠ABC的平分线BE交AD于E,DE=1cm,则BC=4cm.
平行四边形ABCD中,AB=3cm,∠ABC的平分线BE交AD于E,DE=1cm,则BC=4cm.