题目内容
17.观察下列有规律的数:$\frac{1}{2}$,$\frac{1}{6}$,$\frac{1}{12}$,$\frac{1}{20}$,$\frac{1}{30}$,$\frac{1}{42}$…根据规律可知:(1)第8个数是$\frac{1}{72}$,第n个数是$\frac{1}{n(n+1)}$(n是正整数);
(2)$\frac{1}{132}$是第11个数;
(3)计算$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$+…+$\frac{1}{199×200}$.
分析 分子都是1,分母拆成两个连续自然数的乘积,可得规律:第n个数为$\frac{1}{n(n+1)}$.
(1)求得第8个数和第n个数即可;
(2)132=11×12,得出$\frac{1}{132}$是第11个数;
(3)利用$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$拆分计算得出答案即可.
解答 解:(1)第8个数是$\frac{1}{8×9}$=$\frac{1}{72}$,第n个数是$\frac{1}{n(n+1)}$(n是正整数);
(2)$\frac{1}{132}$是第11个数;
(3)$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$+…+$\frac{1}{199×200}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{199}$-$\frac{1}{200}$
=1-$\frac{1}{200}$
=$\frac{199}{200}$.
点评 此题考查数字的变化规律,解题的关键是根据所给出的数据找出之间的运算规律,利用规律解决问题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
9. 如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$(x>0)的图象上,则点E的坐标是( )
如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$(x>0)的图象上,则点E的坐标是( )
 如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$(x>0)的图象上,则点E的坐标是( )
如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$(x>0)的图象上,则点E的坐标是( )| A. | (4,1) | B. | (3,$\frac{4}{3}$) | C. | ($\frac{\sqrt{5}+1}{2}$,$\frac{\sqrt{5}-1}{2}$) | D. | ($\sqrt{6}+\sqrt{2}$,$\sqrt{6}-\sqrt{2}$) |
7.如果等腰三角形的有一个角是80°,那么顶角是( )
| A. | 80° | B. | 20° | C. | 100° | D. | 20°或80° |
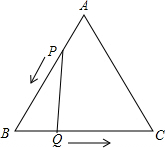 如图所示,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答下列问题:
如图所示,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答下列问题: 将正奇数按如右上图所示规律排列下去.若用有序数对(n,m)表示实数9,则(6,3)表示的数是35.2011是(45,16).
将正奇数按如右上图所示规律排列下去.若用有序数对(n,m)表示实数9,则(6,3)表示的数是35.2011是(45,16).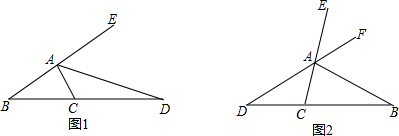
 观察如图所示的三角形数阵,当最下面一行的两个数为多少时,这两个数以及它们上面的数的个数为2015?
观察如图所示的三角形数阵,当最下面一行的两个数为多少时,这两个数以及它们上面的数的个数为2015?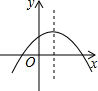 已知二次函数y=ax2+bx+c(x≠0)的图象如图所示,则正比例函数y=(b+c)x的图象与反比例函数y=$\frac{a}{x}$的图象在同一坐标系中可能是( )
已知二次函数y=ax2+bx+c(x≠0)的图象如图所示,则正比例函数y=(b+c)x的图象与反比例函数y=$\frac{a}{x}$的图象在同一坐标系中可能是( )


