题目内容

14．当m=0时，直线（m-1）x+y=4和x-y=3平行．

分析 根据两直线平行，一次项系数之比相等，求出m的值．

解答 解：∵直线（m-1）x+y=4和x-y=3，
∴y=-（m-1）x+4，y=x-3，
∵直线（m-1）x+y=4和x-y=3平行，
∴-（m-1）=1，
解得m=0．
故答案为0．

点评 本题考查了两条直线平行问题，两直线平行，一次项系数之比相等是关键．

练习册系列答案
相关题目
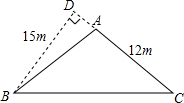4．如图所示，有一块三角形ABC空地，要在这块空地上种植草皮来美化环境，已知这种草皮每平方米售价300元，AC=12m，BD=15m．
（1）购买这种草皮至少需要多少元？
（2）现在学校想到这块空地上种红、黄、白、紫色四种花，而且要保证这四种花的面积相等，画出你的分法．
5．将一个直角三角形ABO放在平面直角坐标系中，如图所示，其中直角顶点O与坐标原点重合，斜边AB与y轴相交于点C．

（1）如图1，当∠A=∠AOC时，试判断∠COB与∠B的大小关系，并说明理由；
（2）如图2，AB的延长线与x轴相交于点E，OD⊥AB于点D，若∠A=∠AEO，∠DOB=∠BOE．求∠ABO的度数；
（3）如图3，在（2）的惰况下，将△ABO绕O点旋转（边AB始终与y轴有交点）时，OF平分∠AOG，CP平分∠OCB，并与OF的反向延长线相交于点P，在旋转过程中，∠P的大小是否发生变化？如果发生变化，求∠P的变化范围；如果不变，求∠P的值．
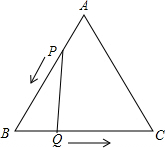2．如图所示，△ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动．设点P的运动时间为t（s），解答下列问题：
（1）当t为何值时，△PBQ是直角三角形？
（2）设四边形APQC的面积为y（cm2），求y（cm2）与t（s）的关系式；是否存在某一时刻t（s），使得四边形APQC的面积有最值？并求最值．
9．下列说法错误的是（　　）
A．一个非零数与其倒数之积为1
B．一个数与其相反数之商为-1
C．若两个数的商为-1，则这两个数互为相反数
D．若两个数的积为1，则这两个数互为倒数
4．观察下列各式：$\frac{{3}^{2}}{{2}^{2}-1}=\frac{3}{2-1}$，$\frac{{4}^{2}}{{3}^{2}-1}=\frac{4}{3-1}$，…，设n表示正整数（n≥3），用含n的代数式表示这个规律为$\frac{（n+1）^{2}}{{n}^{2}-1}$=$\frac{n+1}{n-1}$．
11．化简$\frac{1}{x+1}$-$\frac{x+3}{{x}^{2}-1}$•$\frac{{x}^{2}-2x+1}{{x}^{2}+4x+3}$，其中x+2=$\frac{1}{x}$．
8．某汽车制造公司计划生产A、B两种新型汽车共40辆投放到市场销售．已知A型汽车每辆成本34万元，售价39万元；B型汽车每辆成本42万元，售价50万元．若该公司对此项计划的投资不低于1536万元，不高于1552万元．请解答下列问题：
（1）该公司有哪几种生产方案？
（2）该公司按照哪种方案生产汽车，才能在这批汽车全部售出后，所获利润最大，最大利润是多少？
（3）在（2）的情况下，公司将其中5辆汽车捐赠给了某公益组织，余下的汽车全部售出，这样该公司仍获利44万元，请直接写出该公司把A、B两种型号的汽车各捐赠出几辆？
9．如图，若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$（x＞0）的图象上，则点E的坐标是（　　）
A．（4，1）B．（3，$\frac{4}{3}$）C．（$\frac{\sqrt{5}+1}{2}$，$\frac{\sqrt{5}-1}{2}$）D．（$\sqrt{6}+\sqrt{2}$，$\sqrt{6}-\sqrt{2}$）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网