题目内容
3.去年鱼塘里饲养鱼苗10千尾,平均每千尾鱼的产量为1000kg.今年计划继续向鱼塘里投放鱼苗,预计每多投放鱼苗1千尾,每千尾鱼的产量将减少50kg.(1)因考虑节省投入资金,今年应投放鱼苗多少千尾?才能使总产量达到10450kg.
(2)今年应投放鱼苗多少千尾?才能使总产量最大?最大总产量是多少?
分析 (1)设今年投放鱼苗x千尾,根据等量关系:总产量达到10450千克,列出方程求解即可;
(2)根据题意得y=(1000-50x)(10+x),通过配方即可求解.
解答 解:(1)设今年投放鱼苗x千尾,根据题意得
(1000-50x)(10+x)=10450,
解这个方程得x1=1,x2=9.
答:今年投放鱼苗1千尾或9千尾,可以使总产量达到10450千克.
(2)设今年投放鱼苗x千尾,总产量为y千克,根据题意得
y=(1000-50x)(10+x)=-50(x-5)2+11250,
当x=5时,y取最大值,最大值为y=11250.
答:当该水产养殖中心今年投放5千尾鱼苗时,可以达到最大总产量,此时最大总产量为11250千克.
点评 考查了一元二次方程的应用,二次函数的运用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.某学校兴趣小组的同学进行社会实践,经过市场调查,整理出某种商品在第x天(1≤x≤80)天的售价与销量的相关信息如下表:
已知该商品的进价为每件20元,设该商品的每天销售利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于5400元?
| 时间x(天) | 1≤x<45 | 45≤x≤80 |
| 售价(元/件) | x+40 | 80 |
| 每天销量(件) | 200-2x | |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于5400元?
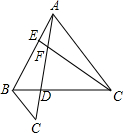 如图,已知等边△ABC,AE=BD,CE、AD交于点F,过点B作BG∥CE,BG交AD的延长线于点G,求证:
如图,已知等边△ABC,AE=BD,CE、AD交于点F,过点B作BG∥CE,BG交AD的延长线于点G,求证: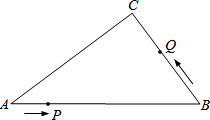 如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.
如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.