题目内容
8.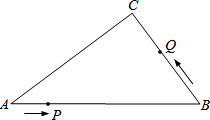 如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.
如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.(1)设点P的运动时间为x(秒),△PBQ的面积为y(cm2),当△PBQ存在时,求y与x的函数关系式,并写出自变量x的取值范围;
(2)当x=5秒时,在直线PQ上是否存在一点M,使△BCM得周长最小?若存在,求出最小周长;若不存在,请说明理由.
(3)当点Q在BC边上运动时,是否存在x,使得以△PBQ的一个顶点为圆心作圆时,另外两个顶点均在这个圆上?若存在,求出x的值;不存在,说明理由.
分析 (1)先求得AC=8,BC=6,当点Q在BC上时,如图1所示:过点Q作QD⊥AB,垂足为D,从而可知:QD=$\frac{4}{5}$QB=$\frac{8}{5}x$,PB=10-x,然后利用三角形的面积公式得到y与x的函数关系;当点Q在AC上时,如图2所示:过点Q作QD⊥AB,垂足为D,则QD=$\frac{3}{5}$AQ=$\frac{3}{5}$(14-2x),然后利用三角形的面积公式得到y与x的函数关系;
(2)当x=5时,可证明PQ为△ABC的中位线,从而可证明PQ是AC的垂直平分线,当点M与P重合时,△BCM的周长最小;
(3)由题意得△PBQ为等腰三角形,然后根据PQ=PB时、BQ=BP时、当QP=QB时分别画出图形进行计算即可.
解答 解:(1)①如图1所示:过点Q作QD⊥AB,垂足为D.
设AC=4k,BC=3k(k>0),由勾股定理得:AC2+BC2=AB2,即(3k)2+(4k)2=100
解得:k=2.
∴AC=8,BC=6.
∴sin∠CBA=$\frac{4}{5}$.
设点P的运动时间为x(秒),则QB=2x,AP=x,BP=10-x.
∵QD⊥AB,
∴QD=$\frac{4}{5}$QB=$\frac{8}{5}x$.
∴S△PBQ=$\frac{1}{2}PB•QD$=$\frac{1}{2}×(10-x)×\frac{8x}{5}$.
∴y=-$-\frac{4}{5}$x2+8x(0<x≤3)
②如图2所示:过点Q作QD⊥AB,垂足为D.
根据题意可知:AQ=14-2x,PB=10-x.
∵QD⊥BA,
∴QD=$\frac{3}{5}$AQ=$\frac{3}{5}$(14-2x).
∴${S}_{△QPB}=\frac{1}{2}PB•QD$=$\frac{1}{2}×(10-x)×\frac{3}{5}(14-2x)$=$\frac{3}{5}$x2-$\frac{51}{5}x+42$(3<x<7).
∴y=$\frac{3}{5}$x2-$\frac{51}{5}x+42$(3<x<7).
综上所述,y与x的函数关系式为y=$\left\{\begin{array}{l}{-\frac{4}{5}{x}^{2}+8x(0<x≤3)}\\{\frac{3}{5}{x}^{2}-\frac{51}{5}x+42(3<x<7)}\end{array}\right.$.
(2)存在.
理由:如图③所示:
∵AQ=14-2x=14-10=4,AP=x=5,
∵AC=8,AB=10,
∴PQ是△ABC的中位线,
∴PQ∥AB,
∴PQ⊥AC.
∴PQ是AC的垂直平分线,
∴PC=AP=5,
∴当点M与P重合时,△BCM的周长最小.
∴△BCM的周长为:MB+BC+MC=PB+BC+PC=5+6+5=16.
∴△BCM的周长最小值为16.
(3)由题意得△PBQ为等腰三角形.
①如图4所示:PQ=PB时,过点P作PD⊥BC,垂足为D.
∵PQ=PB,PD⊥QB,
∴BD=$\frac{1}{2}$QB=x.
∴$\frac{PB}{BD}=\frac{AB}{BC}$,即$\frac{10-x}{x}=\frac{10}{6}$.
解得:x=$\frac{15}{4}$>3(舍去).
②如图5所示;BQ=BP时.
∵QB=2x,PB=10-x,
∴2x=10-x.
解得;x=$\frac{10}{3}$>3(舍去).
③如图6所示:当QP=QB时,过点Q作QD⊥PB,垂足为D.
∵QP=PB,QD⊥PB,
∴PD=BD=$\frac{1}{2}(10-x)$=5-$\frac{1}{2}x$.
∴$\frac{DB}{BC}=\frac{QB}{AB}$,即$\frac{5-\frac{1}{2}x}{6}=\frac{2x}{10}$.
解得:x=$\frac{50}{17}$.
综上所述,存在满足题意得x,此时x=$\frac{50}{17}$.
点评 本题主要考查的是求函数的关系式、勾股定理的应用、锐角三角函数的定义、等腰三角形的性质、线段垂直平分线的性质、三角形的中位线定理,分类讨论是解题的关键.

| A. | 3 | B. | 6 | C. | 2$\sqrt{3}$ | D. | $\sqrt{6}$ |
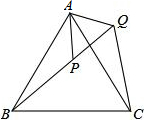 如图,△ABC是等边三角形,点P△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,求证:AP=AQ.
如图,△ABC是等边三角形,点P△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,求证:AP=AQ.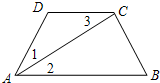 如图已知∠1=∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由.
如图已知∠1=∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由. 一座抛物线型拱桥如图所示,桥下水面宽度是6m,拱高是3m,当水面上升1m后,水面的宽度是多少?(结果精确到0.1m)
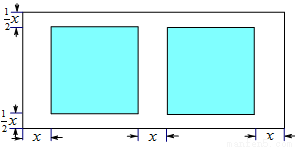
一座抛物线型拱桥如图所示,桥下水面宽度是6m,拱高是3m,当水面上升1m后,水面的宽度是多少?(结果精确到0.1m)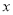 米,当
米,当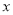 为何值时,花圃的面积之和为72米
为何值时,花圃的面积之和为72米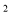 ?
?