题目内容
15.某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件.根据销售经验,提高单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.如果售价为x元,总利润为y元.(1)写出y与x的函数关系式;
(2)当售价x为多少元时,总利润为y最大,最大值是多少元?
分析 (1)根据总利润=每件日用品的利润×可卖出的件数,即可得到y与x的函数关系式;
(2)利用公式法可得二次函数的最值.
解答 解:(1)∵销售单价为x元,销售利润为y元.
根据题意,得y=(x-20)[400-20(x-30)]=(x-20)(1000-20x)=-20x2+1400x-20000,
∴y与x的函数关系式为:y=-20x2+1400x-20000;
(2)∵y=-20x2+1400x-20000;
当x=-$\frac{1400}{2×(-2)}$=35时,y最大=4500,
∴售价x为35元时,总利润y最大,最大值是4500元.
点评 本题考查了二次函数的应用,二次函数的最值,得到半月内可卖出日用品的件数是解决本题的难点.

练习册系列答案
相关题目
8.下列语句正确的是( )
| A. | 无限小数都是无理数 | B. | 带根号的数都是无理数 | ||
| C. | 无理数都是无限小数 | D. | 无理数的平方是无理数 |
10. 如图,△ABC绕点C按顺时针旋转15°到△DEC,若点A恰好在DE上,AC⊥DE,则∠BAE的度数为( )
如图,△ABC绕点C按顺时针旋转15°到△DEC,若点A恰好在DE上,AC⊥DE,则∠BAE的度数为( )
 如图,△ABC绕点C按顺时针旋转15°到△DEC,若点A恰好在DE上,AC⊥DE,则∠BAE的度数为( )
如图,△ABC绕点C按顺时针旋转15°到△DEC,若点A恰好在DE上,AC⊥DE,则∠BAE的度数为( )| A. | 15° | B. | 55° | C. | 65° | D. | 75° |
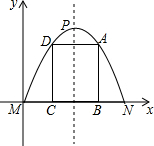 如图,有一块铁皮,拱形边缘呈抛物线状,MN=4dm,抛物线顶点到MN的距离是4dm.要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在MN上,A、D落在抛物线上.建立如图所示的平面直角坐标系,
如图,有一块铁皮,拱形边缘呈抛物线状,MN=4dm,抛物线顶点到MN的距离是4dm.要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在MN上,A、D落在抛物线上.建立如图所示的平面直角坐标系, 一座抛物线型拱桥如图所示,桥下水面宽度是6m,拱高是3m,当水面上升1m后,水面的宽度是多少?(结果精确到0.1m)
一座抛物线型拱桥如图所示,桥下水面宽度是6m,拱高是3m,当水面上升1m后,水面的宽度是多少?(结果精确到0.1m) =3
=3 ,则n的值是( )
,则n的值是( )  的一个根,则代数式
的一个根,则代数式 的值是__________.
的值是__________.