题目内容
14.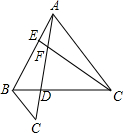 如图,已知等边△ABC,AE=BD,CE、AD交于点F,过点B作BG∥CE,BG交AD的延长线于点G,求证:
如图,已知等边△ABC,AE=BD,CE、AD交于点F,过点B作BG∥CE,BG交AD的延长线于点G,求证:(1)AD=CE;
(2)∠BAD=∠ACE;
(3)∠CFD=60°;
(4)BG+DF=CE.
分析 (1)根据等腰三角形的性质得到AB=AC=BC,∠ABC=∠BAC=∠ACB=60°,推出△ABD≌△ACE,根据全等三角形的性质即可得到结论;
(2)根据全等三角形的性质于是得到结论;
(3)由于∠BAD=∠ACE,根据外角的性质和等量代换即可得到结论;
(4)延长CE到M,使CM=AG,连接AM,推出△BAG≌△CAM(SAS),根据全等三角形的性质得到∠G=∠M,AM=BG,根据平分线的性质得到∠G=∠AFM,等量代换得到∠M=∠AFM,根据等腰三角形的性质得到AM=AF,等量代换即可得到结论.
解答 解:(1)在等边△ABC中,
∵AB=AC=BC,
∠ABC=∠BAC=∠ACB=60°,
在△ABD与△ACE中,
$\left\{\begin{array}{l}{AB=BD}\\{∠ABD=∠CAE}\\{BD=AE}\end{array}\right.$,
∴△ABD≌△ACE,
∴AD=CE;
(2)∵△ABD≌△ACE,
∴∠BAD=∠ACE;
(3)∵∠BAD=∠ACE,
∴∠CDF=∠CAF+∠ACF=∠CAF+∠EAF=60°;
(4)延长CE到M,使CM=AG,连接AM,
在△BAG和△CAM中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAG=ACM}\\{AG=CM}\end{array}\right.$,
∴△BAG≌△CAM(SAS),
∴∠G=∠M,AM=BG,
∵BG∥CE,
∴∠G=∠AFM,
∴∠M=∠AFM,
∴AM=AF,
∵AM=BG,
∴AF=BG,
∴BG+DF=AF+DF=AD=CE.
点评 本题考查了等腰三角形的性质,等边三角形的性质,全等三角形的性质和判定的应用,能正确根据知识点进行推理是解此题的关键.

练习册系列答案
相关题目
8.下列语句正确的是( )
| A. | 无限小数都是无理数 | B. | 带根号的数都是无理数 | ||
| C. | 无理数都是无限小数 | D. | 无理数的平方是无理数 |
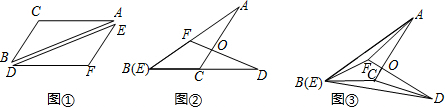
 如图,在△ABC中,点D为BC边上-点,∠BAD=∠CAE=∠CDE,AC=AE.
如图,在△ABC中,点D为BC边上-点,∠BAD=∠CAE=∠CDE,AC=AE.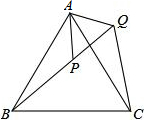 如图,△ABC是等边三角形,点P△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,求证:AP=AQ.
如图,△ABC是等边三角形,点P△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,求证:AP=AQ.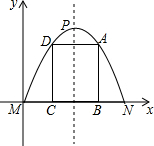 如图,有一块铁皮,拱形边缘呈抛物线状,MN=4dm,抛物线顶点到MN的距离是4dm.要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在MN上,A、D落在抛物线上.建立如图所示的平面直角坐标系,
如图,有一块铁皮,拱形边缘呈抛物线状,MN=4dm,抛物线顶点到MN的距离是4dm.要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在MN上,A、D落在抛物线上.建立如图所示的平面直角坐标系, 的一个根,则代数式
的一个根,则代数式 的值是__________.
的值是__________.