题目内容
3．计算：$\frac{x}{x-2}$-$\frac{x+2}{{x}^{2}-4}$．分析 原式通分并利用同分母分式的减法法则计算即可得到结果．
解答 解：原式=$\frac{x（x+2）}{（x+2）（x-2）}$-$\frac{x+2}{（x+2）（x-2）}$=$\frac{（x+2）（x-1）}{（x+2）（x-2）}$=$\frac{x-1}{x-2}$．
点评 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
13．为了了解1000名初三毕业班学生一分钟跳绳次数的情况，某校抽取了一部分初三毕业生进行一分钟跳绳次数的测试，将所得数据进行处理，可得频率分布表：
（1）这个问题中，总体是1000名初三毕业班学生每分钟跳绳次数的全体； 样本容量a=100；
（2）第四小组的频数b=40，频率c=0.40；
（3）若次数在110次（含110次）以上为达标，试估计该校初三毕业生一分钟跳绳的达标率是多少？
（1）这个问题中，总体是1000名初三毕业班学生每分钟跳绳次数的全体； 样本容量a=100；
（2）第四小组的频数b=40，频率c=0.40；
（3）若次数在110次（含110次）以上为达标，试估计该校初三毕业生一分钟跳绳的达标率是多少？
| 组别 | 分 组 | 频数 | 频率 |
| 1 | 89.5～99.5 | 4 | 0.04 |
| 2 | 99.5～109.5 | 3 | 0.03 |
| 3 | 109.5～119.5 | 45 | 0.45 |
| 4 | 119.5～129.5 | b | c |
| 5 | 129.5～139.5 | 6 | 0.06 |
| 6 | 139.5～149.5 | 2 | 0.02 |
| 合 计 | a | 1.00 | |
14．
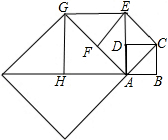正方形ABCD的边长为1，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去，第n个正方形边长为（ ）
正方形ABCD的边长为1，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去，第n个正方形边长为（ ）| A． | 2n | B． | 2n-1 | C． | （$\sqrt{2}$）n | D． | （$\sqrt{2}$）n-1 |
如图，点A（1，4），B（-4，a）在双曲线y=$\frac{k}{x}$图象上，直线AB分别交x轴，y轴于C、D，过点A作AE⊥x轴，垂足为E，过点B作BF⊥y轴，垂足为F，连接AF、BE交于点G．
如图，在平面直角坐标系中，已知点A、B的坐标分别为（8，0）、（0，2$\sqrt{3}$），C是AB的中点，过点C作y轴的垂线，垂足为D，动点P从点D出发，沿DC向点C匀速运动，过点P作x轴的垂线，垂足为E，连接BP、EC．当BP所在直线与EC所在直线第一次垂直时，点P的坐标为（1，$\sqrt{3}$）．
12．
如图，直线a∥b，△ABC为等腰直角三角形，∠BAC=90°，则∠1的度数是（ ）
如图，直线a∥b，△ABC为等腰直角三角形，∠BAC=90°，则∠1的度数是（ ）| A． | 22.5° | B． | 36° | C． | 45° | D． | 90° |
