Question

14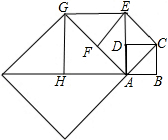．正方形ABCD的边长为1，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去，第n个正方形边长为（　　）

• A． 2ⁿ
• B． 2^n-1
• C． （$\sqrt{2}$）ⁿ
• D． （$\sqrt{2}$）^n-1

Answer 1

分析 先求出第一个正方形边长、第二个正方形边长、第三个正方形边长，…探究规律后，即可解决问题．

解答 解：第一个正方形的边长为1=（$\sqrt{2}$）⁰；
第二个正方形的边长为$\sqrt{2}$=（$\sqrt{2}$）¹
第三个正方形的边长为2=（$\sqrt{2}$）²，
第四个正方形的边长为2$\sqrt{2}$=（$\sqrt{2}$）³，
…
第n个正方形的边长为（$\sqrt{2}$）^n-1，
故选B．

点评 本题考查了正方形的性质，以及勾股定理在直角三角形中的运用，考查了学生找规律的能力，本题中找到a_n的规律是解题的关键．