题目内容
10.学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
分析 (1)设一只A型节能灯的售价是x元,一只B型节能灯的售价是y元,根据:“1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元”列方程组求解即可;
(2)首先根据“A型节能灯的数量不多于B型节能灯数量的3倍”确定自变量的取值范围,然后得到有关总费用和A型灯的只数之间的关系得到函数解析式,确定函数的最值即可.
解答 解:(1)设一只A型节能灯的售价是x元,一只B型节能灯的售价是y元,
根据题意,得:$\left\{\begin{array}{l}{x+3y=26}\\{3x+2y=29}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=5}\\{y=7}\end{array}\right.$,
答:一只A型节能灯的售价是5元,一只B型节能灯的售价是7元;
(2)设购进A型节能灯m只,总费用为W元,
根据题意,得:W=5m+7(50-m)=-2m+350,
∵-2<0,
∴W随m的增大而减小,
又∵m≤3(50-m),解得:m≤37.5,
而m为正整数,
∴当m=37时,W最小=-2×37+350=276,
此时50-37=13,
答:当购买A型灯37只,B型灯13只时,最省钱.
点评 此题主要考查了二元一次方程组的应用以及一次函数的应用等知识,根据题意得出正确的等量关系是解题关键.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
20.桌面上有甲、乙、丙三个杯子,三杯内原本均装有一些水.先将甲杯的水全部倒入丙杯,此时丙杯的水量为原本甲杯内水量的2倍多40毫升;再将乙杯的水全部倒入丙杯,此时丙杯的水量为原本乙杯内水量的3倍少180毫升.若过程中水没有溢出,则原本甲、乙两杯内的水量相差多少毫升?( )
| A. | 80 | B. | 110 | C. | 140 | D. | 220 |
18.下列能用平方差公式计算得是( )
| A. | (-x+y)(x-y) | B. | (y-1)(-1-y) | C. | (x-2)(y+2) | D. | (2x+y)(2y-x) |
5.若不等式组$\left\{\begin{array}{l}{x>a}\\{x-3≤0}\end{array}\right.$,只有三个正整数解,则a的取值范围为( )
| A. | 0≤a<1 | B. | 0<a<1 | C. | 0<a≤1 | D. | 0≤a≤1 |
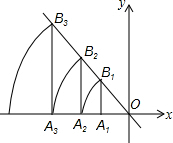 如图,直线l:y=-$\frac{4}{3}$x,点A1坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2016的坐标为(-$\frac{{5}^{2015}}{{3}^{2014}}$,0).
如图,直线l:y=-$\frac{4}{3}$x,点A1坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2016的坐标为(-$\frac{{5}^{2015}}{{3}^{2014}}$,0). 如图,△ABC中,DE是BC的垂直平分线,若AC=7cm,△ABE的周长为13cm,则AB的长为6cm.
如图,△ABC中,DE是BC的垂直平分线,若AC=7cm,△ABE的周长为13cm,则AB的长为6cm.