题目内容
2.解不等式组:$\left\{\begin{array}{l}{5x+1>2(x-4)}\\{\frac{1}{4}x-2≤\frac{3x+1}{2}}\end{array}\right.$.分析 分别求出各不等式的解集,再求出其公共解集即可.
解答 解:$\left\{\begin{array}{l}5x+1>2(x-4)①\\ \frac{1}{4}x-2≤\frac{3x+1}{2}②\end{array}\right.$,
由①,得x>-3,
由②,得x≥-2,
所以不等式组的解集是x≥-2.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
13.如图所示,用量角器度量∠AOB,可以读出∠AOB的度数为( )


| A. | 45° | B. | 55° | C. | 125° | D. | 135° |
17.当0<x<1时,x2、x、$\frac{1}{x}$的大小顺序是( )
| A. | x2$<x<\frac{1}{x}$ | B. | $\frac{1}{x}$<x<x2 | C. | $\frac{1}{x}<{x}^{2}$<x | D. | x<x2<$\frac{1}{x}$ |
7.不等式2(x+1)<3x的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
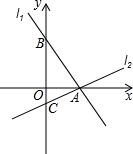 如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.
如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.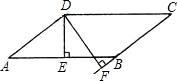 如图所示,?ABCD的周长是10$\sqrt{3}$+6$\sqrt{2}$,AB的长是5$\sqrt{3}$,DE⊥AB于E,DF⊥CB交CB的延长线于点F,DE的长是3,则DF的长为$\frac{5\sqrt{6}}{2}$.
如图所示,?ABCD的周长是10$\sqrt{3}$+6$\sqrt{2}$,AB的长是5$\sqrt{3}$,DE⊥AB于E,DF⊥CB交CB的延长线于点F,DE的长是3,则DF的长为$\frac{5\sqrt{6}}{2}$.