题目内容
15.荔枝是深圳的特色水果,小明的妈妈先购买了2千克桂味和3千克糯米糍,共花费90元;后又购买了1千克桂味和2千克糯米糍,共花费55元.(每次两种荔枝的售价都不变)(1)求桂味和糯米糍的售价分别是每千克多少元;
(2)如果还需购买两种荔枝共12千克,要求糯米糍的数量不少于桂味数量的2倍,请设计一种购买方案,使所需总费用最低.
分析 (1)设桂味的售价为每千克x元,糯米糍的售价为每千克y元;根据单价和费用关系列出方程组,解方程组即可;
(2)设购买桂味t千克,总费用为W元,则购买糯米糍(12-t)千克,根据题意得出12-t≥2t,得出t≤4,由题意得出W=-5t+240,由一次函数的性质得出W随t的增大而减小,得出当t=4时,W的最小值=220(元),求出12-4=8即可.
解答 解:(1)设桂味的售价为每千克x元,糯米糍的售价为每千克y元;
根据题意得:$\left\{\begin{array}{l}{2x+3y=90}\\{x+2y=55}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=15}\\{y=20}\end{array}\right.$;
答:桂味的售价为每千克15元,糯米糍的售价为每千克20元;
(2)设购买桂味t千克,总费用为W元,则购买糯米糍(12-t)千克,
根据题意得:12-t≥2t,
∴t≤4,
∵W=15t+20(12-t)=-5t+240,
k=-5<0,
∴W随t的增大而减小,
∴当t=4时,W的最小值=220(元),此时12-4=8;
答:购买桂味4千克,糯米糍8千克时,所需总费用最低.
点评 本题考查了一次函数的应用、二元一次方程组的应用;根据题意方程方程组和得出一次函数解析式是解决问题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
5.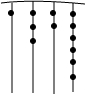 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )| A. | 84 | B. | 336 | C. | 510 | D. | 1326 |
3.下列图案既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.不等式2(x+1)<3x的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
4.若关于x的不等式组$\left\{\begin{array}{l}{x>a}\\{x<2}\end{array}\right.$恰有3个整数解,则字母a的取值范围是( )
| A. | a≤-1 | B. | -2≤a<-1 | C. | a<-1 | D. | -2<a≤-1 |

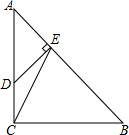 如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE,求:
如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE,求: