题目内容
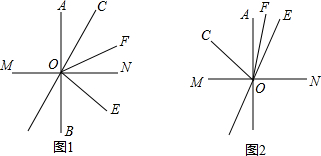
已知:如图,直线AB⊥直线MN于点O,OC⊥OE,射线OF平分∠AOE.
(1)若OD是OC的反射向延长线,
①当∠BOD=20°和40°时,分别直接写出∠BOE和∠COF的度数;
②猜想∠COF和∠BOE之间的数量关系?并说明理由;
(2)若将∠COE绕点O旋转至图2的位置,OD是OE的反向延长线,试问(1)中∠COF和∠BOE之间的数量关系是否发生变化?说明理由.
(1)若OD是OC的反射向延长线,
①当∠BOD=20°和40°时,分别直接写出∠BOE和∠COF的度数;
②猜想∠COF和∠BOE之间的数量关系?并说明理由;
(2)若将∠COE绕点O旋转至图2的位置,OD是OE的反向延长线,试问(1)中∠COF和∠BOE之间的数量关系是否发生变化?说明理由.

考点:垂线,角平分线的定义
专题:
分析:(1)根据角的互余关系容易求出结果,得出结论;
(2)先求出∠MOC=∠AOE=∠BOD,再求出∠AOF=∠EOF,容易得出∠BOE=180°-∠BOD=180°-∠AOE=2(90°-EOF)=2∠COF.
(2)先求出∠MOC=∠AOE=∠BOD,再求出∠AOF=∠EOF,容易得出∠BOE=180°-∠BOD=180°-∠AOE=2(90°-EOF)=2∠COF.
解答:解:(1)①当∠BOD=20°时,∠BOE=70°,∠COF=35°°;
当∠BOD=40°时,∠BOE=50°,∠COF=25°;
②∠BOE=2∠COF;
∵AB⊥MN,OC⊥MN,
∴∠AON=∠DOE=∠COE=90°,
∴∠AOC+∠CON=90°,∠CON+∠EON=90°,
∴∠AOC=∠EON,
∵OF平分∠AOE,
∴∠AOF=∠EOF,
∴∠COF=∠FON,
∵∠BOE+∠EON=90°,
∴∠BOE=∠CON=2∠COF.
(2)∵AB⊥MN,OC⊥MN,
∴∠AON=∠AOM=∠COE=90°,
∴∠MOC=∠AOE=∠BOD,
∵OF平分∠AOE,
∴∠AOF=∠EOF,
∵∠BOE=180°-∠BOD=180°-∠AOE=2(90°-EOF)=2∠COF.
当∠BOD=40°时,∠BOE=50°,∠COF=25°;
②∠BOE=2∠COF;
∵AB⊥MN,OC⊥MN,
∴∠AON=∠DOE=∠COE=90°,
∴∠AOC+∠CON=90°,∠CON+∠EON=90°,
∴∠AOC=∠EON,
∵OF平分∠AOE,
∴∠AOF=∠EOF,
∴∠COF=∠FON,
∵∠BOE+∠EON=90°,
∴∠BOE=∠CON=2∠COF.
(2)∵AB⊥MN,OC⊥MN,
∴∠AON=∠AOM=∠COE=90°,
∴∠MOC=∠AOE=∠BOD,
∵OF平分∠AOE,
∴∠AOF=∠EOF,
∵∠BOE=180°-∠BOD=180°-∠AOE=2(90°-EOF)=2∠COF.
点评:本题考查了垂线的性质和角平分线的定义;弄清各个角之间的数量关系是解题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
下列说法中正确的有( )
①等角的余角相等;②两直线平行,同旁内角相等;③相等的角是对顶角;④同位角相等;⑤直角三角形中两锐角互余.
①等角的余角相等;②两直线平行,同旁内角相等;③相等的角是对顶角;④同位角相等;⑤直角三角形中两锐角互余.
| A、1个 | B、2个 | C、3个 | D、4个 |
在Rt△ABC中,∠C=90°,若tanA=
,则sinA等于( )
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在△ABC中,∠C=90°,D在BC上一点,AC=2,CD=1,记∠CAD=α.
如图,在△ABC中,∠C=90°,D在BC上一点,AC=2,CD=1,记∠CAD=α. 如图,AB∥CD,∠1=∠A,求证:EF∥CD.
如图,AB∥CD,∠1=∠A,求证:EF∥CD.