题目内容
A城有蔬菜200t,B城有蔬菜300t,现要把这些蔬菜全部运往C,D两乡,从A城往C,D两乡运蔬菜的费用分别用20元/t和25元/t;从B城往C,D两乡运蔬菜的费用分别为15元/t和24元/t,现C乡需要蔬菜240t,D乡需要蔬菜260t,假设从A城运往C乡xt蔬菜,怎样调运可使总运费最少?最少的总运费是多少元?
考点:一次函数的应用
专题:
分析:设总运费为y元,A城运往C乡的蔬菜为xt,则运往D乡的蔬菜为(200-x)t;B城运往C、D乡的蔬菜分别为(240-x)t和(60+x)t,然后根据总运费和运输量的关系列出方程式,最后根据一次函数的性质及x的取值范围求出y的最小值.
解答:解:设总运费为y元,A城运往C乡的蔬菜为xt,则运往D乡的蔬菜为(200-x)t;B城运往C、D乡的蔬菜分别为(240-x)t和[260-(200-x)]=(60+x)t,由题意,得y=20x+25(200-x)+15(240-x)+24(60+x),
化简得y=4x+10040(0≤x≤200),
∵k=4>0,
∴y随x的增大而增大,
∴当x=0时,y的最小值10040.
答:从A城运往C乡0吨,运往D乡200吨;从B城运往C乡240吨,运往D乡60吨,此时总运费最少,总运费最小值是10040元.
化简得y=4x+10040(0≤x≤200),
∵k=4>0,
∴y随x的增大而增大,
∴当x=0时,y的最小值10040.
答:从A城运往C乡0吨,运往D乡200吨;从B城运往C乡240吨,运往D乡60吨,此时总运费最少,总运费最小值是10040元.
点评:本题考查了一次函数的应用:根据实际问题列出一次函数关系式,然后利用一次函数的性质解决问题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 如图,已知∠1=∠2,求证:∠3=∠4.
如图,已知∠1=∠2,求证:∠3=∠4.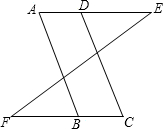 如图,在:①AB∥CD;②AD∥BC;③∠A=∠C中,请你选取其中的两个作为条件,另一个作为结论,写出一个正确命题,并证明其正确性.
如图,在:①AB∥CD;②AD∥BC;③∠A=∠C中,请你选取其中的两个作为条件,另一个作为结论,写出一个正确命题,并证明其正确性. 如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BD=5cm,BC=4cm,则点D到直线AB的距离是
如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BD=5cm,BC=4cm,则点D到直线AB的距离是