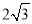题目内容
定义:如果过三角形一个顶点的直线与对边所在直线相交,得到的三角形中有一个与原三角形相似,那么我们称这样的直线为三角形的相似线.
如图1,△ABC中,直线CD与AB交于点D,若△ACD∽△ABC,则称直线CD是△ABC的相似线.
解决问题:
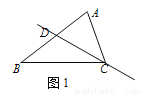
已知:如图2,在△ABC中,∠BAC>∠ACB >∠ABC.
求作:△ABC的相似线.
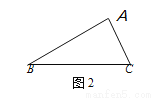
(1)小明用如下方法作出△ABC的一条相似线:
作法:如图3,①作△ABC的外接圆⊙O;
②以C为圆心,AC的长为半径画弧,与⊙O交于点P;
③连接AP,交BC于点D.
则直线AD为△ABC的相似线.
请你证明小明的作法的正确性.
(2)过A点还有其它的△ABC的相似线,请你参考(1)中的作法与结论,利用尺规作图,在图3中再作出一条△ABC的相似线AE;(写出作法,保留作图痕迹,不要证明)
(3)若△ABC中,∠BAC=90°,则△ABC中过A点的相似线有 条,过B点的相似线有 条.
练习册系列答案
相关题目


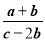 的值是 ______ .
的值是 ______ . B.
B.  C.
C.  D.
D. 

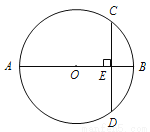
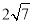 B. 10 C.
B. 10 C. 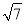 D. 5
D. 5

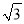 C. 4 D.
C. 4 D.