题目内容
4.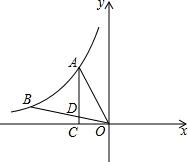 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )| A. | 1 | B. | -$\frac{8}{3}$ | C. | -$\frac{9}{8}$ | D. | -$\frac{9}{4}$ |
分析 作BM⊥OC于M,连接AB,设A(a,$\frac{k}{a}$)则B(3a,$\frac{k}{3a}$),先求出△AOB面积,再证明梯形ABMC面积等于△ABO面积,列出方程即可解决.
解答 解:如图作BM⊥OC于M,连接AB,
∵BD=2OD,S△AOD=1,
∴S△ABD=2,S△AOB=3,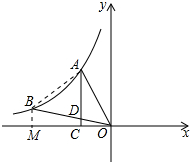 设A(a,$\frac{k}{a}$)则B(3a,$\frac{k}{3a}$),
设A(a,$\frac{k}{a}$)则B(3a,$\frac{k}{3a}$),
∵S△AOB=S四边形ABMO-S△BMO═S四边形ABMO-S△AOC=S梯形ABMC
∴$\frac{1}{2}$($\frac{k}{a}$+$\frac{k}{3a}$)•(-2a)=3,
∴k=-$\frac{9}{4}$,
故选D.
点评 本题考查反比例函数系数k的几何意义,解题的关键是设未知数,用方程思想去思考问题,属于中考常考题型.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
12. 如图,PA切⊙于点A,OP交⊙O于点B,且点B为OP的中点,弦AC∥OP.若OP=2,则图中阴影部分的面积为( )
如图,PA切⊙于点A,OP交⊙O于点B,且点B为OP的中点,弦AC∥OP.若OP=2,则图中阴影部分的面积为( )
 如图,PA切⊙于点A,OP交⊙O于点B,且点B为OP的中点,弦AC∥OP.若OP=2,则图中阴影部分的面积为( )
如图,PA切⊙于点A,OP交⊙O于点B,且点B为OP的中点,弦AC∥OP.若OP=2,则图中阴影部分的面积为( )| A. | $\frac{π}{3}-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{π}{3}-\frac{{\sqrt{3}}}{4}$ | C. | $\frac{π}{6}-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{π}{6}-\frac{{\sqrt{3}}}{4}$ |
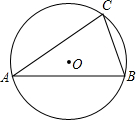 如图,△ABC内接于⊙O,∠BAC=30°,BC=$\sqrt{3}$,则⊙O的半径等于$\sqrt{3}$.
如图,△ABC内接于⊙O,∠BAC=30°,BC=$\sqrt{3}$,则⊙O的半径等于$\sqrt{3}$.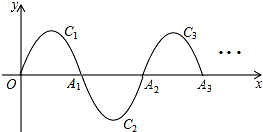 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,…如此进行下去,得到一条“波浪线”.若点P(41,m)在此“波浪线”上,则m的值为( )
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,…如此进行下去,得到一条“波浪线”.若点P(41,m)在此“波浪线”上,则m的值为( )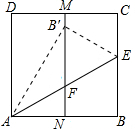 如图,正方形ABCD中,M,N分别是DC、AB的中点,沿过点A的直线折叠,使点B落在MN上,落点为B′,折痕交BC于点E,交MN于点F,再把这个正方形展开,若B′F=3cm,则AB=3$\sqrt{3}$cm.
如图,正方形ABCD中,M,N分别是DC、AB的中点,沿过点A的直线折叠,使点B落在MN上,落点为B′,折痕交BC于点E,交MN于点F,再把这个正方形展开,若B′F=3cm,则AB=3$\sqrt{3}$cm.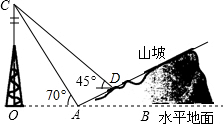 如图,小李在山坡坡脚A处测得他所在小区信号塔塔尖C的仰角为70°,在山坡上的点D处有一坐台,在点D处测得点C的仰角为45°,经侧量知信号塔塔底O距离山坡坡脚A的距离为200米,坡面的铅直高度与水平宽度的比为1:2,试根据以上数据求出信号塔塔尖:C与坐台D的距离.(结果保留整数,参考数据:cos70°≈0.34,sin70°≈0.94,tan70°≈2.75,$\sqrt{2}$=1.41)
如图,小李在山坡坡脚A处测得他所在小区信号塔塔尖C的仰角为70°,在山坡上的点D处有一坐台,在点D处测得点C的仰角为45°,经侧量知信号塔塔底O距离山坡坡脚A的距离为200米,坡面的铅直高度与水平宽度的比为1:2,试根据以上数据求出信号塔塔尖:C与坐台D的距离.(结果保留整数,参考数据:cos70°≈0.34,sin70°≈0.94,tan70°≈2.75,$\sqrt{2}$=1.41) 如图,射线OA∥BC,BO=BC,∠OBC=50°,若将射线OA绕点O顺时针方向旋转锐角x°,射线OA恰好经过点C,则x=50.
如图,射线OA∥BC,BO=BC,∠OBC=50°,若将射线OA绕点O顺时针方向旋转锐角x°,射线OA恰好经过点C,则x=50.