题目内容
19.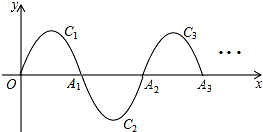 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,…如此进行下去,得到一条“波浪线”.若点P(41,m)在此“波浪线”上,则m的值为( )
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,…如此进行下去,得到一条“波浪线”.若点P(41,m)在此“波浪线”上,则m的值为( )| A. | 2 | B. | -2 | C. | 0 | D. | $\frac{9}{4}$ |
分析 先解方程-x(x-3)=0得A1(3,0),OA1=3,利用旋转的性质得到A1A2=OA1=3,则OA2=6,A2(6,0),所以C2的解析式为y=(x-3)(x-6)(3≤x≤6),利用此规律可判断角标为奇数的抛物线开口向下,角标为偶数的抛物线开口向上,由于OA13=39,OA14=42,则A13(39,0),A14(42,0),于是可利用交点式写出C14的解析式为y=(x-39)(x-42)(39≤x≤42),然后把点P(41,m)代入可计算出m的值.
解答 解:当y=0时,-x(x-3)=0,解得x1=0,x2=3,则A1(3,0),OA1=3,
∵C1绕A1旋转180°得到C2,
∴A1A2=OA1=3,则OA2=6,A2(6,0),
∴C2的解析式为y=(x-3)(x-6)(3≤x≤6),
同样可得OA13=39,OA14=42,则A13(39,0),A14(42,0),
∴C14的解析式为y=(x-39)(x-42)(39≤x≤42),
∴点P(41,m)在抛物线C14上,
当x=41时,m=2×(-1)=-2.
故选B.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.解决本题的关键是能利用交点式写出每段抛物线的解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.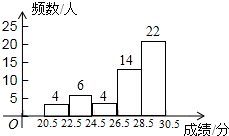 九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )
九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )
 九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )
九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )| A. | 80% | B. | 70% | C. | 92% | D. | 86% |
4.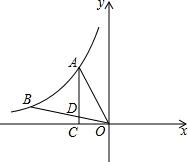 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )
 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )| A. | 1 | B. | -$\frac{8}{3}$ | C. | -$\frac{9}{8}$ | D. | -$\frac{9}{4}$ |
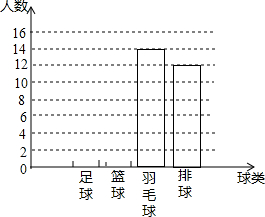 为了了解某校学生对球类运动的爱好情况,采用抽样的方法,从足球、篮球、羽毛球、排球等四个方面调查了若干名学生,并绘制成不完整的条形图.已知最喜欢篮球的人数占调查人数的32%,最喜欢排球的人数是最喜欢足球人数的1.5倍.
为了了解某校学生对球类运动的爱好情况,采用抽样的方法,从足球、篮球、羽毛球、排球等四个方面调查了若干名学生,并绘制成不完整的条形图.已知最喜欢篮球的人数占调查人数的32%,最喜欢排球的人数是最喜欢足球人数的1.5倍.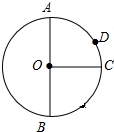 AB是⊙O的直径,且AB=2,OC⊥AB,垂足为点O,弧AD:弧DC=2:1,在OC上有一动点P,则PA+PD的最小值为$\sqrt{3}$.
AB是⊙O的直径,且AB=2,OC⊥AB,垂足为点O,弧AD:弧DC=2:1,在OC上有一动点P,则PA+PD的最小值为$\sqrt{3}$.