题目内容
10. 如图,射线OA∥BC,BO=BC,∠OBC=50°,若将射线OA绕点O顺时针方向旋转锐角x°,射线OA恰好经过点C,则x=50.
如图,射线OA∥BC,BO=BC,∠OBC=50°,若将射线OA绕点O顺时针方向旋转锐角x°,射线OA恰好经过点C,则x=50.
分析 根据等腰三角形性质可得底角∠BCO度数,由平行线的性质知旋转角∠AOC=∠BCO,可得答案.
解答 解:如图连接OC,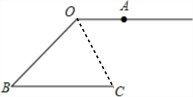
∵∠B=50°,BO=BC,
∴∠BCO=$\frac{180°-∠B}{2}$=65°,
又∵OA∥BC,
∴∠AOC=∠BCO=50°,即x=50,
故答案为:50.
点评 本题主要考查等腰三角形性质和平行线的性质,准确识别旋转变换中的旋转角是解题的前提,熟练掌握等腰三角形和平行线性质是关键.

练习册系列答案
相关题目
4.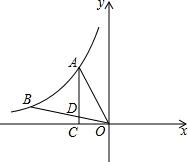 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )
 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过A,B,过A点作x轴的垂线,垂足为C,连接OA,OB,线段OB交AC于点D,若BD=2OD,△AOD的面积为1,则k的值为( )| A. | 1 | B. | -$\frac{8}{3}$ | C. | -$\frac{9}{8}$ | D. | -$\frac{9}{4}$ |
15.函数y=$\frac{k}{x}$的图象经过点(2,3),则k=( )
| A. | 2 | B. | 3 | C. | 6 | D. | -6 |
2.已知反比例函数y=$\frac{6}{x}$,当-3<x<-1时,y的取值范围是( )
| A. | y<0 | B. | -3<y<-1 | C. | -6<y<-2 | D. | 2<y<6 |
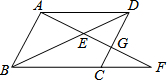 如图,平行四边形ABCD中,E是BD上一点,AE的延长线与BC的延长线交于F,与CD交于G,若AE=4,EG=3,则EF=$\frac{16}{3}$.
如图,平行四边形ABCD中,E是BD上一点,AE的延长线与BC的延长线交于F,与CD交于G,若AE=4,EG=3,则EF=$\frac{16}{3}$. 如图.抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线上位于直线AB上方的一点(不与点A,B重合),连接AD,BD.
如图.抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线上位于直线AB上方的一点(不与点A,B重合),连接AD,BD. 某学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了如图所示的条形统计图,则30名学生参加活动的次数的中位数是2次.
某学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了如图所示的条形统计图,则30名学生参加活动的次数的中位数是2次.